
已知函數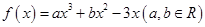 在點
在點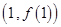 處的切線方程為
處的切線方程為 .
.
⑴求函數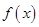 的解析式;
的解析式;
⑵若對于區間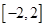 上任意兩個自變量的值
上任意兩個自變量的值 都有
都有 ,求實數
,求實數 的最小值;
的最小值;
⑶若過點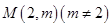 可作曲線
可作曲線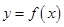 的三條切線,求實數
的三條切線,求實數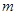 的取值范圍.
的取值范圍.
(1)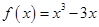 ;(2)4;(3)
;(2)4;(3) .
.
解析試題分析:(1)利用切點處的切線的斜率就是切點處的導數可列關于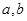 一個的等式,再根據切點既在曲線上又在切線上又可列出關于
一個的等式,再根據切點既在曲線上又在切線上又可列出關于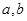 一個的等式,聯立即可解出關于
一個的等式,聯立即可解出關于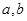 ,從而求出函數
,從而求出函數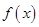 (2)對于區間
(2)對于區間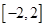 上任意兩個自變量的值
上任意兩個自變量的值 都有
都有 ,可轉化為
,可轉化為 ,再轉化為
,再轉化為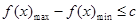 ,而
,而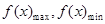 利用導數判斷單調性后易求;(3)可設切點為
利用導數判斷單調性后易求;(3)可設切點為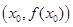 ,求出切線方程后,將
,求出切線方程后,將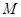 點坐標代入可得關于
點坐標代入可得關于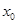 的三次方程,過點
的三次方程,過點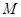 可作曲線
可作曲線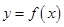 的三條切線,則表示這個方程有三個不同的解,再轉化為三次函數的零點的判斷,可求極值用數形結合的方法解決,這是我們所熟悉的問題.
的三條切線,則表示這個方程有三個不同的解,再轉化為三次函數的零點的判斷,可求極值用數形結合的方法解決,這是我們所熟悉的問題.
試題解析:⑴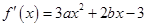 . 2分
. 2分
根據題意,得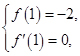 即
即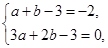 解得
解得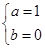 3分
3分
所以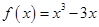 . 4分
. 4分
⑵令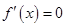 ,即
,即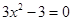 .得
.得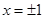 .
.