
設平面向量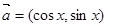 ,
,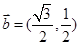 ,函數
,函數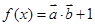 .
.
(Ⅰ)求函數 的值域和函數的單調遞增區間;
的值域和函數的單調遞增區間;
(Ⅱ)當 ,且
,且 時,求
時,求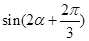 的值.
的值.
(Ⅰ)值域是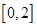 ;單調增區間為
;單調增區間為 ;(Ⅱ)
;(Ⅱ)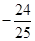
解析試題分析:根據 的特點,利用平面向量的數量積的運算法則化簡,然后利用兩角和的正弦函數公式及特殊角的三角函數值化為一個角的正弦函數,從而確定出
的特點,利用平面向量的數量積的運算法則化簡,然后利用兩角和的正弦函數公式及特殊角的三角函數值化為一個角的正弦函數,從而確定出 的解析式,
的解析式,
根據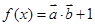 、數量積公式和三角函數恒等變換,求出
、數量積公式和三角函數恒等變換,求出
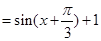 ,在根據正弦函數的性質求出函數
,在根據正弦函數的性質求出函數 的值域;
的值域;
②根據正弦函數的單調區間為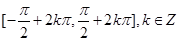 ,列出不等式,求出不等式的解集即可得到
,列出不等式,求出不等式的解集即可得到 的取值范圍即為
的取值范圍即為 的遞增區間;
的遞增區間;
③根據 ,代入
,代入 的解析式中,得到
的解析式中,得到 的值,根據
的值,根據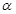 的范圍求出
的范圍求出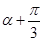 的范圍,利用同角三角函數間的基本關系求出
的范圍,利用同角三角函數間的基本關系求出 的值,把所求的式子利用二倍角的正弦函數公式化簡,將
的值,把所求的式子利用二倍角的正弦函數公式化簡,將 和
和 的值代入即可求出值.
的值代入即可求出值.
試題解析:依題意

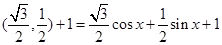 (2分)
(2分)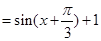 (4分)
(4分)
(Ⅰ) 函數 的值域是
的值域是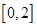 ; (5分)
; (5分)
令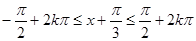 ,解得
,解得 (7分)
(7分)
所以函數 的單調增區間為
的單調增區間為 . (8分)
. (8分)
(Ⅱ)由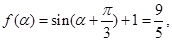 得
得 ,
,
因為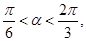 所以
所以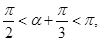 得
得 , (10分)
, (10分)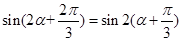

 (12分).
(12分).
考點:1.正弦函數的定義域和值域、正弦函數的單調性;2. 三角函數的恒等變換及化簡求值;3.平面向量數量積的運算.


湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com