
【題目】如圖,在三棱柱![]() 中,平面
中,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 為
為![]() 的中點.
的中點.

(1)求證: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)見解析;(2)![]() .
.
【解析】試題分析:證明線面垂直,只需尋求線線垂直,利用題目提供的面面垂直,可以得到線面垂直,進而說明線線垂直;求二面角可采用建立空間直角坐標系,借助法向量求解,本題需要設![]() ,根據條件求出
,根據條件求出![]() ,再利用法向量求出二面角的余弦.
,再利用法向量求出二面角的余弦.
試題解析:(1)證明:∵![]() ,
, ![]() 為
為![]() 的中點,∴
的中點,∴![]() ,又平面
,又平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,∴
,∴![]() .又
.又![]() ,
, ![]() ,∴
,∴![]() 面
面![]() .
.
(2)方法一:由平面![]() 平面
平面![]() ,作
,作![]() 于
于![]() ,則
,則![]() 面
面![]() .
.
作![]() 于
于![]() ,連
,連![]() ,則
,則![]() ,由
,由![]() ,
, ![]() ,
,
![]() 知
知![]()
![]()
![]() ,而
,而![]() ,
, ![]() ,故
,故![]() ,即
,即![]() .
.
在四邊形![]() 中,設
中,設![]() .
.
則由余弦定理得![]() .
.
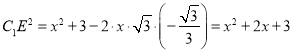 ,設
,設![]() 與
與![]() 交于點
交于點![]() ,則
,則
![]() ,
, ![]() ,而
,而![]()
![]() ,則
,則![]() .
.
于是![]() ,即
,即![]() ,∴
,∴![]() 或
或![]() (舍)
(舍)
容易求得: ![]() ,而
,而![]() .
.
故![]() ,由面
,由面![]() 面
面![]() ,則
,則![]() 面
面![]() ,過
,過![]() 作
作![]() 于
于![]() ,連
,連![]() ,則
,則![]() 為二面角
為二面角![]() 的平面角,由平面幾何知識易得
的平面角,由平面幾何知識易得![]() ,
, ![]() .
.
∴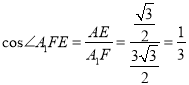 .
.
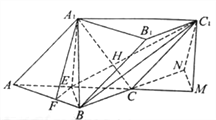
方法二:以![]() 點為原點,
點為原點, ![]() 為
為![]() 軸,過點
軸,過點![]() 與平面
與平面![]() 垂直的直線為
垂直的直線為![]() 軸,建立如圖所示的空間直角坐標系,設
軸,建立如圖所示的空間直角坐標系,設![]() ,
, ![]() ,則
,則![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
∴![]() ,
, ![]() .由
.由 ,得
,得![]() ,∴
,∴![]() ,則
,則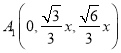 ,
, 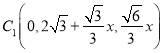 ,于是
,于是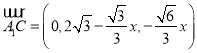 ,
, 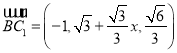 ,
,
∵![]() ,
,
∴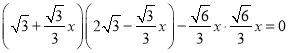 ,即
,即![]() ,解得
,解得![]() 或
或![]() (舍),故
(舍),故![]() ,則
,則![]() ,
, ![]() ,于是
,于是![]() ,
, ![]() ,設平面
,設平面![]() 的法向量為
的法向量為![]() ,則
,則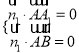 即
即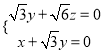 ,取
,取![]() ,則
,則![]() ,∴
,∴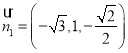 .
.
不妨設平面![]() 的法向量
的法向量![]() ,則
,則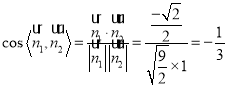 ,
,
故二面角![]() 的余弦值為
的余弦值為![]() .
.



 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中數學 來源: 題型:
【題目】甲、乙兩位同學在高一年級的5次考試中,數學成績統計如莖葉圖所示,若甲、乙兩人的平均成績分別是 ![]() ,則下列敘述正確的是( )
,則下列敘述正確的是( ) 
A.![]() >
> ![]() ,乙比甲成績穩定
,乙比甲成績穩定
B.![]() >
> ![]() ,甲比乙成績穩定
,甲比乙成績穩定
C.![]() <
< ![]() ,乙比甲成績穩定
,乙比甲成績穩定
D.![]() <
< ![]() ,甲比乙成績穩定
,甲比乙成績穩定
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知向量 ![]() =(cosx,cosx),
=(cosx,cosx), ![]() =(sinx,﹣cosx),記函數f(x)=2
=(sinx,﹣cosx),記函數f(x)=2 ![]()
![]() +1,其中x∈R.
+1,其中x∈R.
(Ⅰ)求函數f(x)的最小正周期及函數f(x)的圖象的對稱中心的坐標;
(Ⅱ)若α∈(0, ![]() ),且f(
),且f( ![]() )=
)= ![]() ,求cos2α的值.
,求cos2α的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() (
(![]() )的兩個頂點分別為
)的兩個頂點分別為![]() 和
和![]() ,兩個焦點分別為
,兩個焦點分別為![]() 和
和![]() (
(![]() ),過點
),過點![]() 的直線
的直線![]() 與橢圓相交于另一點
與橢圓相交于另一點![]() ,且
,且![]() .
.
(Ⅰ)求橢圓的離心率;
(Ⅱ)設直線![]() 上有一點
上有一點![]() (
(![]() )在
)在![]() 的外接圓上,求
的外接圓上,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設點P的坐標為(x﹣3,y﹣2).
(1)在一個盒子中,放有標號為1,2,3的三張卡片,現在從盒子中隨機取出一張卡片,記下標號后把卡片放回盒中,再從盒子中隨機取出一張卡片記下標號,記先后兩次抽取卡片的標號分別為x、y,求點P在第二象限的概率;
(2)若利用計算機隨機在區間[0,3]上先后取兩個數分別記為x、y,求點P在第三象限的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,直四棱柱ABCD﹣A1B1C1D1內接于半徑為 ![]() 的半球O,四邊形ABCD為正方形,則該四棱柱的體積最大時,AB的長是( )
的半球O,四邊形ABCD為正方形,則該四棱柱的體積最大時,AB的長是( ) 
A.1
B.![]()
C.![]()
D.2
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知四棱錐P﹣ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形, 且∠DAB=90°,∠ABC=45°,CB= ![]() ,AB=2,PA=1
,AB=2,PA=1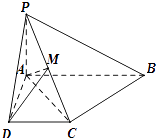
(1)求證:AB∥平面PCD;
(2)求證:BC⊥平面PAC;
(3)若M是PC的中點,求三棱錐C﹣MAD的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《中國詩詞大會》(第二季)亮點頗多,十場比賽每場都有一首特別設計的開場詩詞,在聲光舞美的配合下,百人團齊聲朗誦,別有韻味.若《將進酒》《山居秋暝》《望岳》《送杜少府之任蜀州》和另確定的兩首詩詞排在后六場,且《將進酒》排在《望岳》的前面,《山居秋暝》與《送杜少府之任蜀州》不相鄰且均不排在最后,則后六場的排法有( )
A. ![]() 種 B.
種 B. ![]() 種 C.
種 C. ![]() 種 D.
種 D. ![]() 種
種
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com