
【題目】在數列{an}中,a1=4,nan+1﹣(n+1)an=2n2+2n.
(Ⅰ)求證:數列 ![]() 是等差數列;
是等差數列;
(Ⅱ)求數列 ![]() 的前n項和Sn .
的前n項和Sn .
【答案】解:(I)解法一:(Ⅰ) ![]() 的兩邊同時除以n(n+1), 得
的兩邊同時除以n(n+1), 得 ![]() ,(3分)
,(3分)
所以數列 ![]() 是首項為4,公差為2的等差數列.
是首項為4,公差為2的等差數列.
解法二:依題意,可得 ![]() ,
,
所以 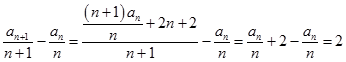 ,
,
即 ![]() ,
,
所以數列 ![]() 是首項為4,公差為2的等差數列.
是首項為4,公差為2的等差數列.
(Ⅱ)由(Ⅰ),得 ![]() ,(7分)
,(7分)
所以 ![]() ,故
,故 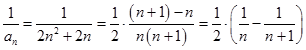 ,
,
所以 ![]()
= ![]()
= ![]()
【解析】(I)解法一: ![]() 的兩邊同時除以n(n+1),
的兩邊同時除以n(n+1), ![]() ,即可證明解法二:依題意,可得
,即可證明解法二:依題意,可得 ![]() ,可得
,可得 ![]() ,即可證明.(Ⅱ)由(Ⅰ),得
,即可證明.(Ⅱ)由(Ⅰ),得 ![]() ,可得
,可得 ![]() ,
, ![]() =
= ![]() .利用裂項求和方法即可得出.
.利用裂項求和方法即可得出.
【考點精析】掌握數列的前n項和和數列的通項公式是解答本題的根本,需要知道數列{an}的前n項和sn與通項an的關系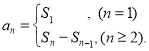 ;如果數列an的第n項與n之間的關系可以用一個公式表示,那么這個公式就叫這個數列的通項公式.
;如果數列an的第n項與n之間的關系可以用一個公式表示,那么這個公式就叫這個數列的通項公式.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】在平面上, ![]() ⊥
⊥ ![]() ,|
,| ![]() |=|
|=| ![]() |=1,
|=1, ![]() =
= ![]() +
+ ![]() .若|
.若| ![]() |<
|< ![]() ,則|
,則| ![]() |的取值范圍是( )
|的取值范圍是( )
A.(0, ![]() ]
]
B.( ![]() ,
, ![]() ]
]
C.( ![]() ,
, ![]() ]
]
D.( ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ln(1+x)﹣ln(1﹣x),給出以下四個命題: ①x∈(﹣1,1),有f(﹣x)=﹣f(x);
②x1 , x2∈(﹣1,1)且x1≠x2 , 有 ![]() ;
;
③x1 , x2∈(0,1),有 ![]() ;
;
④x∈(﹣1,1),|f(x)|≥2|x|.
其中所有真命題的序號是( )
A.①②
B.③④
C.①②③
D.①②③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知正實數a,b,c,函數f(x)=|x+a||x+b|. (Ⅰ)若a=1,b=3,解關于x的不等式f(x)+x+1<0;
(Ⅱ)求證:f(1)f(c)≥16abc.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐A﹣BCD中,平面ABD⊥平面BCD,AB=AD,∠CBD=60°,BD=2BC=4,點E在CD上,DE=2EC. 
(Ⅰ)求證:AC⊥BE;
(Ⅱ)若二面角E﹣BA﹣D的余弦值為 ![]() ,求三棱錐A﹣BCD的體積.
,求三棱錐A﹣BCD的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下面幾種推理過程是演繹推理的是 ( )
A. 某校高三(1)班有55人,2班有54人,3班有52人,由此得高三所有班人數超過50人
B. 兩條直線平行,同旁內角互補,如果∠A與∠B是兩條平行直線的同旁內角,則∠A+∠B=180°
C. 由平面三角形的性質,推測空間四邊形的性質
D. 在數列{an}中,a1=1,an=![]() (an-1+
(an-1+![]() )(n≥2),由此歸納出{an}的通項公
)(n≥2),由此歸納出{an}的通項公
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線l的參數方程為 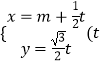 為參數),以坐標原點為極點,以x軸正半軸為極軸建立極坐標系,橢圓C的極坐標方程為
為參數),以坐標原點為極點,以x軸正半軸為極軸建立極坐標系,橢圓C的極坐標方程為 ![]() ,且直線l經過橢圓C的右焦點F.
,且直線l經過橢圓C的右焦點F.
(1)求橢圓C的內接矩形PMNQ面積的最大值;
(2)若直線l與橢圓C交于A,B兩點,求|FA||FB|的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com