
【題目】已知函數![]() 的定義域為(0,+
的定義域為(0,+![]() ),若
),若![]() 在(0,+
在(0,+![]() )上為增函數,則稱
)上為增函數,則稱![]() 為“一階比增函數”;若
為“一階比增函數”;若![]() 在(0,+
在(0,+![]() )上為增函數,則稱
)上為增函數,則稱![]() 為”二階比增函數”。我們把所有“一階比增函數”組成的集合記為
為”二階比增函數”。我們把所有“一階比增函數”組成的集合記為![]() 1,所有“二階比增函數”組成的集合記為
1,所有“二階比增函數”組成的集合記為![]() 2。
2。
(1)已知函數![]() ,若
,若![]() ∈
∈![]() 1,求實數
1,求實數![]() 的取值范圍,并證明你的結論;
的取值范圍,并證明你的結論;
(2)已知0<a<b<c,![]() ∈
∈![]() 1且
1且![]() 的部分函數值由下表給出:
的部分函數值由下表給出:
|
|
|
|
|
|
|
| t | 4 |
求證:![]() ;
;
(3)定義集合![]() ,且存在常數k,使得任取x∈(0,+
,且存在常數k,使得任取x∈(0,+![]() ),
),![]() <k},請問:是否存在常數M,使得任意的
<k},請問:是否存在常數M,使得任意的![]() ∈
∈![]() ,任意的x∈(0,+
,任意的x∈(0,+![]() ),有
),有![]() <M成立?若存在,求出M的最小值;若不存在,說明理由。
<M成立?若存在,求出M的最小值;若不存在,說明理由。
【答案】(1)![]() ≤0;(2)見解析;(3)0
≤0;(2)見解析;(3)0
【解析】
(1)由![]() ∈
∈![]() ,即
,即![]() 在(0,+
在(0,+![]() )是增函數,利用單調性的定義求解即可;
)是增函數,利用單調性的定義求解即可;
(2)由f(x)∈Ω1,取0<x1<x2<x1+x2,可得![]() .由表格可知:f(a)=d,f(b)=d,f(c)=t,f(a+b+c)=4,0<a<b<c<a+b+c,利用“一階比增函數”可得
.由表格可知:f(a)=d,f(b)=d,f(c)=t,f(a+b+c)=4,0<a<b<c<a+b+c,利用“一階比增函數”可得![]() ,再利用不等式的性質即可得出;
,再利用不等式的性質即可得出;
(3)根據“二階比增函數”先證明f(x)≤0對x∈(0,+∞)成立.再證明f(x)=0在(0,+∞)上無解.即可得出.
(1)解:因為![]() ∈
∈![]() ,即
,即![]() 在(0,+
在(0,+![]() )是增函數,
)是增函數,
當![]() ≤0,函數顯然為增函數;
≤0,函數顯然為增函數;
當![]() >0,
>0,
任取![]() ,則
,則![]()
![]()
![]() .
.
![]() ,
,![]()
當![]() ≤0,
≤0,![]() ,
,![]() , 函數為增函數
, 函數為增函數
當![]() >0,
>0,
當![]() 時,
時,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,即
,即![]() ,所以
,所以![]() 在
在![]() 上為減函數.
上為減函數.
當![]() 時,
時,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,即
,即![]() ,所以
,所以![]() 在
在![]() 上為增函數.
上為增函數.
所以![]() ≤0,
≤0,
(2)因為![]() ∈
∈![]() ,且0<a<b<c<a+b+c,
,且0<a<b<c<a+b+c,
所以![]() ,所以
,所以![]() ,
,
同理可證![]() ,
,![]() ,
,
三式相加得![]() ,所以
,所以![]() 。
。
因為![]() ,所以
,所以![]() ,而0<a<b,所以d<0,所以
,而0<a<b,所以d<0,所以![]() 。
。
(3)因為集合![]() ,且存在常數k,使得任取x∈(0,+
,且存在常數k,使得任取x∈(0,+![]() ),
),![]() <k},
<k},
所以![]()
![]() ∈
∈![]() ,存在常數k,使得
,存在常數k,使得![]() <k對x∈(0,+
<k對x∈(0,+![]() )成立。
)成立。
我們先證明![]() ≤0對x∈(0,+
≤0對x∈(0,+![]() )成立:假設
)成立:假設![]()
![]() ∈(0,+
∈(0,+![]() ),使得
),使得![]() >0,記
>0,記![]() >0,
>0,
因為![]() 是二階比增函數,即
是二階比增函數,即![]() 是增函數。所以當x>
是增函數。所以當x>![]() 時,
時,![]() >
>![]() ,所以
,所以![]()
![]() ,
,
所以一定可以找到一個![]() >
>![]() ,使得
,使得![]() >
>![]() >k,這與
>k,這與![]() <k對
<k對![]() ∈(0,+
∈(0,+![]() )成立矛盾,
)成立矛盾,
![]() ≤0對x∈(0,+
≤0對x∈(0,+![]() )成立,所以
)成立,所以![]()
![]() ∈
∈![]() ,
,![]() ≤0對x∈(0,+
≤0對x∈(0,+![]() )成立。
)成立。
下面我們證明![]() 在(0,+
在(0,+![]() )上無解:
)上無解:
假設存在![]() >0,使得
>0,使得![]() =0,則因為
=0,則因為![]() 是二階增函數,即
是二階增函數,即![]() 是增函數,
是增函數,
一定存在![]() >
>![]() >0,
>0,![]() >
>![]() ,這與上面證明的結果矛盾。所以
,這與上面證明的結果矛盾。所以![]() 在(0,+
在(0,+![]() )上無解。
)上無解。
綜上,我們得到![]()
![]() ∈
∈![]() ,
,![]() <0對
<0對![]() ∈(0,+
∈(0,+![]() )成立,
)成立,
所以存在常數M≥0,使得![]()
![]() ∈
∈![]() ,
,![]() x∈(0,+
x∈(0,+![]() ),有
),有![]() M成立,
M成立,
又令![]() =
=![]() (
(![]() >0),則
>0),則![]() <0對x∈(0,+
<0對x∈(0,+![]() )成立,
)成立,
又有![]() 在(0,+
在(0,+![]() )上是增函數,所以
)上是增函數,所以![]() ,
,
而任取常數k<0,總可以找到一個![]() >0,使得
>0,使得![]() >
>![]() 時,有
時,有![]() >k,所以M的最小值為0。
>k,所以M的最小值為0。


科目:高中數學 來源: 題型:
【題目】設函數![]() 的定義域為
的定義域為![]() ,若存在閉區間
,若存在閉區間![]() ,使得函數
,使得函數![]() 滿足:①
滿足:①![]() 在
在![]() 上是單調函數;②
上是單調函數;②![]() 在
在![]() 上的值域是
上的值域是![]() ,則稱區間
,則稱區間![]() 是函數
是函數![]() 的“和諧區間”.下列結論錯誤的是( )
的“和諧區間”.下列結論錯誤的是( )
A. 函數![]() 存在“和諧區間”
存在“和諧區間”
B. 函數![]() 不存在“和諧區間”
不存在“和諧區間”
C. 函數![]() 存在“和諧區間”
存在“和諧區間”
D. 函數![]() (
(![]() 且
且![]() )不存在“和諧區間”
)不存在“和諧區間”
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解學生的課外閱讀時間情況,某學校隨機抽取了50人進行統計分析,把這50人每天閱讀的時間(單位:分鐘)繪制成頻數分布表,如下表所示:
閱讀時間 | [0,20) | [20,40) | [40,60) | [60,80) | [80,100) | [100,120] |
人數 | 8 | 10 | 12 | 11 | 7 | 2 |
若把每天閱讀時間在60分鐘以上(含60分鐘)的同學稱為“閱讀達人”,根據統計結果中男女生閱讀達人的數據,制作出如圖所示的等高條形圖:

(1)根據已知條件完成2x2列聯表;
男生 | 女生 | 總計 | |
閱讀達人 | |||
非閱讀達人 | |||
總計 |
(2)并判斷是否有![]() 的把握認為“閱讀達人”跟性別有關?
的把握認為“閱讀達人”跟性別有關?
附:參考公式![]()
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數,f(x)=|x﹣a|
(Ⅰ)當a=2,解不等式,f(x)≥5﹣|x﹣1|;
(Ⅱ)若f(x)≤1的解集為[0,2],![]() +
+![]() =a(m>0,n>0),求證:m+2n≥4.
=a(m>0,n>0),求證:m+2n≥4.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,圓C的參數方程![]() (φ為參數).以O為極點,x軸的非負半軸為極軸建立極坐標系.
(φ為參數).以O為極點,x軸的非負半軸為極軸建立極坐標系.
(Ⅰ)求圓C的極坐標方程;
(Ⅱ)直線l的極坐標方程是ρ(sinθ+![]() cosθ)=3
cosθ)=3![]() , 射線OM:θ=
, 射線OM:θ=![]() 與圓C的交點為O,P,與直線l的交點為Q,求線段PQ的長.
與圓C的交點為O,P,與直線l的交點為Q,求線段PQ的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() 是偶函數.
是偶函數.
(1)求![]() 的值;
的值;
(2)若函數![]() 的圖象在直線
的圖象在直線![]() 上方,求
上方,求![]() 的取值范圍;
的取值范圍;
(3)若函數![]() ,
,![]() ,是否存在實數
,是否存在實數![]() 使得
使得![]() 的最小值為0?若存在,求出
的最小值為0?若存在,求出![]() 的值,若不存在,請說明理由.
的值,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列關于回歸分析的說法中錯誤的有( )個
(1). 殘差圖中殘差點所在的水平帶狀區域越寬,則回歸方程的預報精確度越高.
(2). 回歸直線一定過樣本中心![]() 。
。
(3). 兩個模型中殘差平方和越小的模型擬合的效果越好。
(4) .甲、乙兩個模型的![]() 分別約為0.88和0.80,則模型乙的擬合效果更好.
分別約為0.88和0.80,則模型乙的擬合效果更好.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】禽流感一直在威脅我們的生活,某疾病控制中心為了研究禽流感病毒繁殖個數![]() (個)隨時間
(個)隨時間![]() (天)變化的規律,收集數據如下:
(天)變化的規律,收集數據如下:
天數 | 1 | 2 | 3 | 4 | 5 | 6 |
繁殖個數 | 6 | 12 | 25 | 49 | 95 | 190 |
作出散點圖可看出樣本點分布在一條指數型函數![]() 的周圍.
的周圍.
保留小數點后兩位數的參考數據:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]()
(1)求出![]() 關于
關于![]() 的回歸方程(保留小數點后兩位數字);
的回歸方程(保留小數點后兩位數字);
(2)已知![]() ,估算第四天的殘差.
,估算第四天的殘差.
參考公式: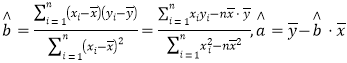
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com