
【題目】甲、乙兩艘輪船駛向一個不能同時停泊兩艘輪船的碼頭,它們在一晝夜內任何時刻到達是等可能的.
(1)已知甲船上有男女乘客各3名,現(xiàn)從中任選3人出來做某件事情,求所選出的人中恰有一位女乘客的概率;
(2)如果甲船的停泊時間為4小時,乙船的停泊時間為2小時,求它們中的任何一條船不需要等待碼頭空出的概率.
【答案】
(1)解:記男乘客分別為1,2,3,記女乘客分別為4,5,6,從中任取3人有123,124,125,126,134,135,136,145,146,156,234,235,236,245,246,256,345,346,356,456,共20種取法,其中恰含一女乘客的有124,125,126,134,135,136,234,235,236共9種,
∴所求概率P= ![]()
(2)解:當甲船的停泊時間為4小時,乙船的停泊時間為2小時,兩船不需等待碼頭空出,則滿足x﹣y≥2或y﹣x≥4.
設在上述條件時“兩船不需等待碼頭空出”為事件B,畫出區(qū)域如圖:  ,
,
P(B)= ![]() =
= ![]() =
= ![]() .
.

【解析】(1)利用列舉法進行求解即可.(2)利用幾何概型求出對應的面積進行求解即可.
【考點精析】解答此題的關鍵在于理解幾何概型的相關知識,掌握幾何概型的特點:1)試驗中所有可能出現(xiàn)的結果(基本事件)有無限多個;2)每個基本事件出現(xiàn)的可能性相等.


科目:高中數(shù)學 來源: 題型:
【題目】在如圖所示的幾何體中,四邊形DCFE為正方形,四邊形ABCD為等腰梯形,AB∥CD,AC= ![]() ,AB=2BC=2,且AC⊥FB.
,AB=2BC=2,且AC⊥FB. 
(1)求證:平面EAC⊥平面FCB;
(2)若線段AC上存在點M,使AE∥平面FDM,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某同學用“五點法”畫函數(shù)f(x)=Asin(ωx+φ)(ω>0,|φ|< ![]() )在某一個周期內的圖象時,列表并填入了部分數(shù)據(jù),如表:
)在某一個周期內的圖象時,列表并填入了部分數(shù)據(jù),如表:
ωx+φ | 0 |
| π |
| 2π |
x | | | |||
f(x) | 0 | 3 | 0 | ﹣3 | 0 |
(1)請將表中數(shù)據(jù)補充完整,并直接寫出函數(shù)f(x)的解析式;
(2)若將函數(shù)f(x)的圖象上所有點的橫坐標變?yōu)樵瓉淼?倍,縱坐標不變,得到函數(shù)g(x)的圖象,求當x∈[﹣ ![]() ,
, ![]() ]時,函數(shù)g(x)的值域;
]時,函數(shù)g(x)的值域;
(3)若將y=f(x)圖象上所有點向左平移θ(θ>0)個單位長度,得到y(tǒng)=h(x)的圖象,若=h(x)圖象的一個對稱中心為( ![]() ),求θ的最小值.
),求θ的最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)f(x)=1﹣ ![]() 為定義在R上的奇函數(shù).
為定義在R上的奇函數(shù).
(1)求f(x)的解析式;
(2)判斷f(x)的單調性,并用定義證明;
(3)若f(lnm)+f(2lnn)≤1﹣3lnm,求實數(shù)m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)f(x)=sin(ωx+φ)(ω>0,|φ|≤ ![]() ),x=﹣
),x=﹣ ![]() 為f(x)的零點,x=
為f(x)的零點,x= ![]() 為y=f(x)圖象的對稱軸,且f(x)在(
為y=f(x)圖象的對稱軸,且f(x)在( ![]() ,
, ![]() )單調,則ω的最大值為 .
)單調,則ω的最大值為 .
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】將函數(shù)f(x)=sin(2x+φ)(0<φ<π)的圖象向左平移 ![]() 個單位后得到函數(shù)y=g(x)的圖象,若y=g(x)是偶函數(shù),則φ= .
個單位后得到函數(shù)y=g(x)的圖象,若y=g(x)是偶函數(shù),則φ= .
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知雙曲線實軸長為6,一條漸近線方程為4x﹣3y=0.過雙曲線的右焦點F作傾斜角為 ![]() 的直線交雙曲線于A、B兩點
的直線交雙曲線于A、B兩點
(1)求雙曲線的方程;
(2)求線段AB的中點C到焦點F的距離.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】長方體ABCD﹣A1B1C1D1中,AB=BC=1,AA1=2,E是側棱BB1的中點. 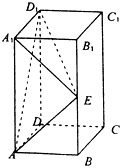
(1)求證:直線AE⊥平面A1D1E;
(2)求二面角E﹣AD1﹣A1的平面角的余弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】將函數(shù)y=sin(x﹣ ![]() )的圖象上所有點的橫坐標伸長到原來的2倍(縱坐標不變),再將所得圖象向左平移
)的圖象上所有點的橫坐標伸長到原來的2倍(縱坐標不變),再將所得圖象向左平移 ![]() 個單位,則所得函數(shù)圖象對應的解析式為( )
個單位,則所得函數(shù)圖象對應的解析式為( )
A.y=sin( ![]() x﹣
x﹣ ![]() )
)
B.y=sin(2x﹣ ![]() )
)
C.y=sin ![]() x
x
D.y=sin( ![]() x﹣
x﹣ ![]() )
)
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com