
【題目】已知函數![]() ,
, ![]() ,其中
,其中![]() …是然對數底數.
…是然對數底數.
(1)若函數![]() 有兩個不同的極值點
有兩個不同的極值點![]() ,
, ![]() ,求實數
,求實數![]() 的取值范圍;
的取值范圍;
(2)當![]() 時,求使不等式
時,求使不等式![]() 在一切實數上恒成立的最大正整數
在一切實數上恒成立的最大正整數![]() .
.
【答案】(1)![]() ;(2)14
;(2)14
【解析】試題分析:(1)函數![]() 有兩個不同的極值點
有兩個不同的極值點![]() ,
, ![]() 得,
得, ![]() 有兩個不同的根
有兩個不同的根![]() ,對
,對![]() 分類討論:當
分類討論:當![]() 時,可得
時,可得![]() 在
在![]() 上遞減,不合題意,
上遞減,不合題意, ![]() ,函數
,函數![]() 在
在![]() 上遞減,在
上遞減,在![]() 上遞增,只需
上遞增,只需![]() ,解出即可得出結果;(2)當
,解出即可得出結果;(2)當![]() 時,由題意可得:不等式
時,由題意可得:不等式![]() 對題意
對題意![]() 恒成立,令
恒成立,令![]() ,令
,令![]() 得
得![]() ,利用單調性可得
,利用單調性可得![]() ,整理得
,整理得![]() ,再研究其單調性即可得出.
,再研究其單調性即可得出.
試題解析:(1)f′(x)=λex﹣2x,據題意得f′(x)=λex﹣2x=0有兩個不同的根x1,x2,當λ≤0時,f′(x)=λex﹣2x≤0,因此f(x)在R上遞減,不合題意,∴λ>0,又f″(x)=λex﹣2,令f″(x)=0,解得![]() ,∴函數f′(x)=λex﹣2x在
,∴函數f′(x)=λex﹣2x在![]() 上遞減,在
上遞減,在![]() 上遞增,∴f′(x)=λex﹣2x=0有兩個不同的根,則
上遞增,∴f′(x)=λex﹣2x=0有兩個不同的根,則![]() ,即
,即![]() ,
,![]() ,解得
,解得![]() .
.
(2)當λ=1時,求使不等式f(x)>g(x)在一切實數上恒成立,即不等式![]() 對任意x恒成立,令
對任意x恒成立,令![]() ,∴
,∴![]() ,令h′(x)=0得
,令h′(x)=0得![]() ,∴函數h(x)在
,∴函數h(x)在![]() 上遞減,在
上遞減,在![]() 上遞增,∴
上遞增,∴![]() ,整理得
,整理得![]() .令
.令![]() ,易得(μ)在(2,+∞)上遞減,若μ=2e2∈(14,15),(2e2)=15﹣2e2>0,若μ=15,
,易得(μ)在(2,+∞)上遞減,若μ=2e2∈(14,15),(2e2)=15﹣2e2>0,若μ=15,![]() ,所以滿足條件的最大整數μ=14.
,所以滿足條件的最大整數μ=14.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】某公司為確定下一年度投入某種產品的宣傳費,需了解年宣傳費![]() (單位:千元)對年銷售量
(單位:千元)對年銷售量![]() (單位:
(單位: ![]() )和年利潤
)和年利潤![]() (單位:千元)的影響.對近8年的年宣傳費
(單位:千元)的影響.對近8年的年宣傳費![]() 和年銷售量
和年銷售量![]() 數據作了初步處理,得到下面的散點圖及一些統計量的值.
數據作了初步處理,得到下面的散點圖及一些統計量的值.

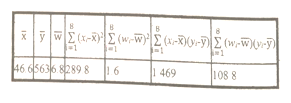
表中![]() .
.
(1)根據散點圖判斷![]() 與
與![]() 哪一個適宜作為年銷售量
哪一個適宜作為年銷售量![]() 關于年宣傳費
關于年宣傳費![]() 的回歸類型?(給出判斷即可,不必說明理由)
的回歸類型?(給出判斷即可,不必說明理由)
(2)根據(1)的判斷結果及表中數據,建立![]() 關于
關于![]() 的回歸方程;
的回歸方程;
(3)已知這種產品的利潤![]() 與
與![]() 的的關系為
的的關系為![]() .根據(2)的結果回答下列問題:
.根據(2)的結果回答下列問題:
(ⅰ)年宣傳費![]() 時,年銷售量及年利潤的預報值是多少?
時,年銷售量及年利潤的預報值是多少?
(ⅱ)年宣傳費![]() 為何值時,年利潤的預報值最大?
為何值時,年利潤的預報值最大?
附:對于一組數據![]() ,其回歸直線
,其回歸直線![]() 的的斜率和截距的最小二乘估計為
的的斜率和截距的最小二乘估計為 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=4cosωxsin(ωx+ ![]() )+a(ω>0)圖象上最高點的縱坐標為2,且圖象上相鄰兩個最高點的距離為π. (Ⅰ)求a和ω的值;
)+a(ω>0)圖象上最高點的縱坐標為2,且圖象上相鄰兩個最高點的距離為π. (Ⅰ)求a和ω的值;
(Ⅱ)求函數f(x)在[0,π]上的單調遞減區間.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)=sin(ωx+φ)(ω>0,|φ|< ![]() )的圖象如圖所示,為了得到g(x)=sinωx的圖象,則只要將f(x)的圖象( )
)的圖象如圖所示,為了得到g(x)=sinωx的圖象,則只要將f(x)的圖象( ) 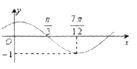
A.向左平移 ![]() 個單位長度
個單位長度
B.向右平移 ![]() 個單位長度
個單位長度
C.向右平移 ![]() 個單位長度
個單位長度
D.向左平移 ![]() 個單位長度
個單位長度
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}是首項為正數的等差數列,a1a2=3,a2a3=15.
(1)求數列{an}的通項公式;
(2)設bn=(an+1)2 ![]() ,求數列{bn}的前n項和Tn .
,求數列{bn}的前n項和Tn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司研發出一款產品,批量生產前先在某城市銷售30天進行市場調查.調查結果發現:日銷量![]() 與天數
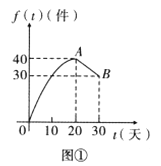
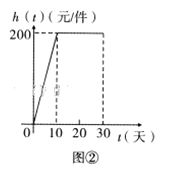
與天數![]() 的對應關系服從圖①所示的函數關系:每件產品的銷售利潤
的對應關系服從圖①所示的函數關系:每件產品的銷售利潤![]() 與天數
與天數![]() 的對應關系服從圖②所示的函數關系.圖①由拋物線的一部分(
的對應關系服從圖②所示的函數關系.圖①由拋物線的一部分(![]() 為拋物線頂點)和線段
為拋物線頂點)和線段![]() 組成.
組成.
(Ⅰ)設該產品的日銷售利潤![]()
![]() ,分別求出
,分別求出![]() ,
, ![]() ,
, ![]() 的解析式,
的解析式,
(Ⅱ)若在30天的銷售中,日銷售利潤至少有一天超過8500元,則可以投入批量生產,該產品是否可以投入批量生產,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖某綜藝節目現場設有A,B,C,D四個觀眾席,現有由5不同顏色的馬甲可供現場觀眾選擇,同一觀眾席上的馬甲的顏色相同,相鄰觀眾席上的馬甲的顏色不相同,則不同的安排方法種數為 . 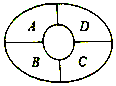
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)= ![]() x3﹣x2+ax+m,其中a>0,如果存在實數t,使f′(t)<0,則f′(t+2)f′(
x3﹣x2+ax+m,其中a>0,如果存在實數t,使f′(t)<0,則f′(t+2)f′( ![]() )的值( )
)的值( )
A.必為正數
B.必為負數
C.必為非負
D.必為非正
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com