
已知函數(shù)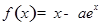
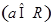 ,
,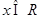 .已知函數(shù)
.已知函數(shù)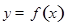 有兩個(gè)零點(diǎn)
有兩個(gè)零點(diǎn)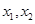 ,且
,且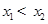 .
.
(1)求 的取值范圍;
的取值范圍;
(2)證明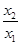 隨著
隨著 的減小而增大;
的減小而增大;
(3)證明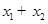 隨著
隨著 的減小而增大.
的減小而增大.
(1)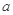 的取值范圍是
的取值范圍是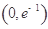 ;(2)詳見(jiàn)試題分析;(3)詳見(jiàn)試題分析.
;(2)詳見(jiàn)試題分析;(3)詳見(jiàn)試題分析.
解析試題分析:(1)先求函數(shù)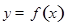 的導(dǎo)數(shù),再分
的導(dǎo)數(shù),再分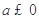 和
和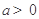 討論
討論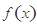 的單調(diào)性,將“函數(shù)
的單調(diào)性,將“函數(shù)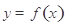 有兩個(gè)零點(diǎn)”等價(jià)轉(zhuǎn)化為如下條件同時(shí)成立:“1°
有兩個(gè)零點(diǎn)”等價(jià)轉(zhuǎn)化為如下條件同時(shí)成立:“1°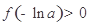 ;2°存在
;2°存在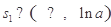 ,滿足
,滿足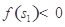 ;3°存在
;3°存在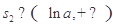 ,滿足
,滿足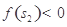 ”,解相應(yīng)的不等式即可求得
”,解相應(yīng)的不等式即可求得 的取值范圍;(2)由
的取值范圍;(2)由 分離出參數(shù)
分離出參數(shù)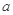 :
: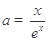 .利用導(dǎo)數(shù)討論
.利用導(dǎo)數(shù)討論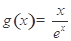 的單調(diào)性即可得:
的單調(diào)性即可得: 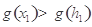 ,從而
,從而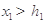 ;類(lèi)似可得
;類(lèi)似可得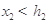 .又由
.又由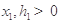 ,得
,得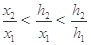 ,最終證得
,最終證得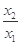 隨著
隨著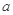 的減小而增大;(3)由
的減小而增大;(3)由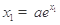 ,
,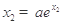 ,可得
,可得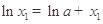 ,
,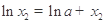 ,作差得
,作差得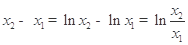 .設(shè)
.設(shè)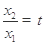 ,則
,則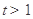 ,且
,且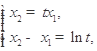 解得
解得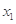 ,
,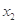 ,可求得
,可求得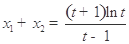 ,構(gòu)造函數(shù)
,構(gòu)造函數(shù)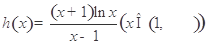 ,利用導(dǎo)數(shù)來(lái)證明
,利用導(dǎo)數(shù)來(lái)證明 隨著
隨著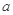 的減小而增大.
的減小而增大.
(1)由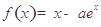 ,可得
,可得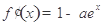 .下面分兩種情況討論:
.下面分兩種情況討論:
(1)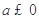 時(shí),
時(shí),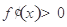 在
在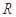 上恒成立,可得
上恒成立,可得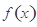 在
在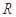 上單調(diào)遞增,不合題意.
上單調(diào)遞增,不合題意.
(2)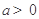 時(shí),由
時(shí),由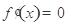 ,得
,得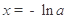 .當(dāng)
.當(dāng)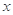 變化時(shí),
變化時(shí),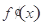 ,
,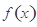 的變化情況如下表:
的變化情況如下表: