
【題目】對于定義在![]() 上的函數(shù)
上的函數(shù)![]() ,若函數(shù)
,若函數(shù)![]() 滿足:①在區(qū)間
滿足:①在區(qū)間![]() 上單調(diào)遞減;②存在常數(shù)p,使其值域為
上單調(diào)遞減;②存在常數(shù)p,使其值域為![]() ,則稱函數(shù)
,則稱函數(shù)![]() 為
為![]() 的“漸近函數(shù)”;
的“漸近函數(shù)”;
(1)證明:函數(shù)![]() 是函數(shù)
是函數(shù)![]()
![]() 的漸近函數(shù),并求此時實數(shù)p的值;
的漸近函數(shù),并求此時實數(shù)p的值;
(2)若函數(shù)![]()
![]()
![]() ,證明:當
,證明:當![]() 時,
時,![]() 不是
不是![]() 的漸近函數(shù).
的漸近函數(shù).
【答案】(1)證明見解析,![]() ;(2)證明見解析;
;(2)證明見解析;
【解析】
(1)通過令![]() ,利用“漸近函數(shù)”的定義逐條驗證即可;(2)通過記
,利用“漸近函數(shù)”的定義逐條驗證即可;(2)通過記![]() ,結(jié)合“漸近函數(shù)”的定義可知
,結(jié)合“漸近函數(shù)”的定義可知![]() ,問題轉(zhuǎn)化為求
,問題轉(zhuǎn)化為求![]() 時,
時,![]() 的最大值問題,進而計算可得
的最大值問題,進而計算可得![]() 的范圍,從而證明結(jié)論.
的范圍,從而證明結(jié)論.
(1)根據(jù)題意,令![]() ,
,
則![]() ,
,
所以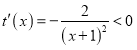 ,
,
所以![]() 在區(qū)間
在區(qū)間![]() 上單調(diào)遞減,且
上單調(diào)遞減,且![]() ,
,
所以![]() ,
,
于是函數(shù)![]() 是函數(shù)
是函數(shù)![]() ,
,![]() 的漸近函數(shù),
的漸近函數(shù),
此時實數(shù)![]() .
.
(2)即![]() ,
,
![]() ,
,
假設函數(shù)![]() ,
,![]() 的漸近函數(shù)是
的漸近函數(shù)是![]() ,
,
則當![]() 時,
時,![]() ,即
,即![]() ,
,
令函數(shù)![]() ,
,![]() ,
,
則![]() ,
,
當![]() 時,
時,![]() ,
,
當![]() 時,
時,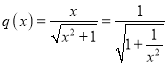 ,在區(qū)間
,在區(qū)間![]() 上單調(diào)遞增,
上單調(diào)遞增,
且![]()
所以![]() ,
,
所以![]() ,
,
所以當![]() 時,
時,![]() 不是
不是![]() 的漸近函數(shù).
的漸近函數(shù).


科目:高中數(shù)學 來源: 題型:
【題目】如圖放置的邊長為1的正方形![]() 沿
沿![]() 軸滾動(向右為順時針,向左為逆時針).設頂點
軸滾動(向右為順時針,向左為逆時針).設頂點![]() 的軌跡方程是
的軌跡方程是![]() ,則關于
,則關于![]() 的最小正周期
的最小正周期![]() 及
及![]() 在其兩個相鄰零點間的圖像與x軸所圍區(qū)域的面積S的正確結(jié)論是( )
在其兩個相鄰零點間的圖像與x軸所圍區(qū)域的面積S的正確結(jié)論是( )
![]()
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】一款擊鼓小游戲的規(guī)則如下:每盤游戲都需要擊鼓三次,每次擊鼓要么出現(xiàn)一次音樂,要么不出現(xiàn)音樂;每盤游戲擊鼓三次后,出現(xiàn)一次音樂獲得10分,出現(xiàn)兩次音樂獲得20分,出現(xiàn)三次音樂獲得100分,沒有出現(xiàn)音樂則扣除200分(即獲得![]() 分).設每次擊鼓出現(xiàn)音樂的概率為
分).設每次擊鼓出現(xiàn)音樂的概率為![]() ,且各次擊鼓出現(xiàn)音樂相互獨立.
,且各次擊鼓出現(xiàn)音樂相互獨立.
(1)設每盤游戲獲得的分數(shù)為![]() ,求
,求![]() 的分布列;
的分布列;
(2)玩三盤游戲,至少有一盤出現(xiàn)音樂的概率是多少?
(3)玩過這款游戲的許多人都發(fā)現(xiàn),若干盤游戲后,與最初的分數(shù)相比,分數(shù)沒有增加反而減少了.請運用概率統(tǒng)計的相關知識分析分數(shù)減少的原因.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() ,離心率為
,離心率為![]() ,直線
,直線![]() 恒過
恒過![]() 的一個焦點
的一個焦點![]() .
.
(1)求![]() 的標準方程;
的標準方程;
(2)設![]() 為坐標原點,四邊形
為坐標原點,四邊形![]() 的頂點均在
的頂點均在![]() 上,
上,![]() 交于
交于![]() ,且
,且![]() ,若直線
,若直線![]() 的傾斜角的余弦值為
的傾斜角的余弦值為![]() ,求直線
,求直線![]() 與
與![]() 軸交點的坐標.
軸交點的坐標.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知動圓過定點![]() ,且在y軸上截得的弦MN的長為8.
,且在y軸上截得的弦MN的長為8.
(1)求動圓圓心的軌跡C的方程;
(2)已知點![]() ,長為
,長為![]() 的線段PQ的兩端點在軌跡C上滑動.當
的線段PQ的兩端點在軌跡C上滑動.當![]() 軸是
軸是![]() 的角平分線時,求直線PQ的方程.
的角平分線時,求直線PQ的方程.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在極坐標系中,已知曲線![]() :
:![]() 和曲線
和曲線![]() :
:![]() ,以極點
,以極點![]() 為坐標原點,極軸為
為坐標原點,極軸為![]() 軸非負半軸建立平面直角坐標系.
軸非負半軸建立平面直角坐標系.
(1)求曲線![]() 和曲線
和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若點![]() 是曲線
是曲線![]() 上一動點,過點
上一動點,過點![]() 作線段
作線段![]() 的垂線交曲線
的垂線交曲線![]() 于點
于點![]() ,求線段
,求線段![]() 長度的最小值.
長度的最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】紅鈴蟲是棉花的主要害蟲之一,能對農(nóng)作物造成嚴重傷害,每只紅鈴蟲的平均產(chǎn)卵數(shù)y和平均溫度x有關,現(xiàn)收集了以往某地的7組數(shù)據(jù),得到下面的散點圖及一些統(tǒng)計量的值.(表中![]() )
)
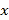
平均溫度 | 21 | 23 | 25 | 27 | 29 | 32 | 35 | ||
平均產(chǎn)卵數(shù) | 7 | 11 | 21 | 24 | 66 | 115 | 325 | ||
|
|
|
|
| |||||
27.429 | 81.286 | 3.612 | 40.182 | 147.714 | |||||
(1)根據(jù)散點圖判斷,![]() 與
與![]() (其中
(其中![]() 自然對數(shù)的底數(shù))哪一個更適宜作為平均產(chǎn)卵數(shù)y關于平均溫度x的回歸方程類型?(給出判斷即可,不必說明理由)并由判斷結(jié)果及表中數(shù)據(jù),求出y關于x的回歸方程.(計算結(jié)果精確到小數(shù)點后第三位)
自然對數(shù)的底數(shù))哪一個更適宜作為平均產(chǎn)卵數(shù)y關于平均溫度x的回歸方程類型?(給出判斷即可,不必說明理由)并由判斷結(jié)果及表中數(shù)據(jù),求出y關于x的回歸方程.(計算結(jié)果精確到小數(shù)點后第三位)
(2)根據(jù)以往統(tǒng)計,該地每年平均溫度達到28℃以上時紅鈴蟲會造成嚴重傷害,需要人工防治,其他情況均不需要人工防治記該地每年平均溫度達到28℃以上的概率為![]() .
.
①記該地今后5年中,恰好需要3次人工防治的概率為![]() ,求
,求![]() 的最大值,并求出相應的概率p.
的最大值,并求出相應的概率p.
②當![]() 取最大值時,記該地今后5年中,需要人工防治的次數(shù)為X,求X的數(shù)學期望和方差.
取最大值時,記該地今后5年中,需要人工防治的次數(shù)為X,求X的數(shù)學期望和方差.
附:線性回歸方程系數(shù)公式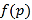 .
.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com