
【題目】已知函數![]() ,
,![]() .
.
(1)求證:存在唯一的實數![]() ,使得直線
,使得直線![]() 與曲線
與曲線![]() 相切;
相切;
(2)若![]() ,
,![]() ,求證:
,求證:![]() .
.
(注:![]() 為自然對數的底數.)
為自然對數的底數.)
【答案】(1)見解析;(2)見解析
【解析】
(1)曲線![]() 在
在![]() 處的切線為
處的切線為![]() ,所以
,所以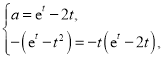 只需證明
只需證明![]() 有唯一解即可.
有唯一解即可.
(2) 要證![]() ,即證
,即證![]() ,設
,設![]() ,即
,即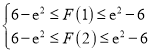 ,只要證明
,只要證明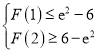 ,然后構造函數,討論單調性,分析函數的最值,即可證明.
,然后構造函數,討論單調性,分析函數的最值,即可證明.
證明:(1)由![]() 知,在
知,在![]() 處的切線為
處的切線為![]() ,
,
當該直線為![]() 時,可得
時,可得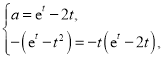
所以![]() ,所以
,所以![]() ,
,
令![]() ,則當
,則當![]() 時,
時,![]() ,
,
所以![]() 在
在![]() 單調遞增,
單調遞增,
而![]() ,
,![]() ,所以存在唯一的實數
,所以存在唯一的實數![]() (
(![]() ),
),
使得![]() ,相應的
,相應的![]() 也是唯一的,
也是唯一的,
即存在唯一-的實數![]() ,使得直線
,使得直線![]() 與曲線
與曲線![]() 相切.
相切.
(2)要證![]() ,即證
,即證![]() ,
,
令![]() ,對于確定的
,對于確定的![]() ,
,![]() 是一次函數,只要證明,
是一次函數,只要證明,
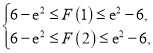
注意到對于同一![]() ,
,![]() ,所以只要證明
,所以只要證明

先證明①:記![]() ,則
,則![]() ,
,
令![]() ,因為
,因為![]() ,所以
,所以![]() ,
,
由此可知![]() 在區間
在區間![]() 遞減,在區間
遞減,在區間![]() 遞增.
遞增.
又因為![]() ,
,![]() ,
,![]() ,
,
所以,在區間![]() 上存在唯一實數
上存在唯一實數![]() ,使得
,使得![]() .
.
故在區間![]() ,
,![]() 遞減,在區間
遞減,在區間![]() ,
,![]() 遞增.
遞增.
于是![]() .①得證.
.①得證.
再證明②:記![]() ,
,
當![]() 時,利用不等式
時,利用不等式![]() 得,
得,
![]() ;
;
當![]() 時,利用不等式
時,利用不等式![]() (
(![]() )得
)得
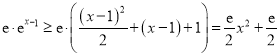 ,
,
于是![]() ,
,
其中二次函數![]() 開口向上,對稱軸為
開口向上,對稱軸為![]() ,
,
當![]() 時,
時,![]() 最小值為
最小值為![]() ,
,
所以![]() .
.
綜上,不等式①②均成立.
所以,當![]() ,對任意的
,對任意的![]() ,總有
,總有![]() .
.


科目:高中數學 來源: 題型:
【題目】很多關于整數規律的猜想都通俗易懂,吸引了大量的數學家和數學愛好者,有些猜想已經被數學家證明,如“費馬大定理”,但大多猜想還未被證明,如“哥德巴赫猜想”、“角谷猜想”.“角谷猜想”的內容是:對于每一個正整數,如果它是奇數,則將它乘以![]() 再加1;如果它是偶數,則將它除以
再加1;如果它是偶數,則將它除以![]() ;如此循環,最終都能夠得到
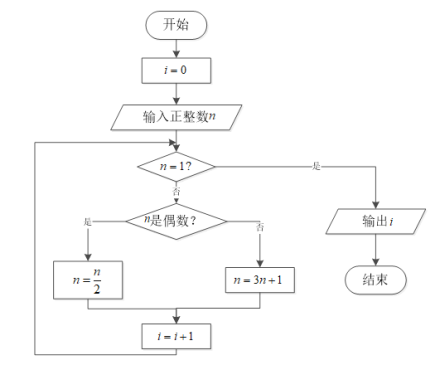
;如此循環,最終都能夠得到![]() .下圖為研究“角谷猜想”的一個程序框圖.若輸入
.下圖為研究“角谷猜想”的一個程序框圖.若輸入![]() 的值為
的值為![]() ,則輸出i的值為( )
,則輸出i的值為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知橢圓
中,已知橢圓![]() 的左頂點為
的左頂點為![]() ,右焦點為
,右焦點為![]() ,過原點
,過原點![]() 的直線(與坐標軸不重合)與橢圓
的直線(與坐標軸不重合)與橢圓![]() 交于點
交于點![]() 、
、![]() ,直線
,直線![]() 、
、![]() 分別與
分別與![]() 軸交于點
軸交于點![]() 、
、![]() .
.
(1)若![]() ,求點
,求點![]() 的橫坐標;
的橫坐標;
(2)設直線![]() 、
、![]() 的斜率分別為
的斜率分別為![]() 、
、![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中心在原點的橢圓E的一個焦點與拋物線![]() 的焦點關于直線
的焦點關于直線![]() 對稱,且橢圓E與坐標軸的一個交點坐標為
對稱,且橢圓E與坐標軸的一個交點坐標為![]() .
.
(1)求橢圓E的標準方程;
(2)過點![]() 的直線l(直線的斜率k存在且不為0)交E于A,B兩點,交x軸于點P點A關于x軸的對稱點為D,直線BD交x軸于點Q.試探究
的直線l(直線的斜率k存在且不為0)交E于A,B兩點,交x軸于點P點A關于x軸的對稱點為D,直線BD交x軸于點Q.試探究![]() 是否為定值?請說明理由.
是否為定值?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】工廠質檢員從生產線上每半個小時抽取一件產品并對其某個質量指標![]() 進行檢測,一共抽取了
進行檢測,一共抽取了![]() 件產品,并得到如下統計表.該廠生產的產品在一年內所需的維護次數與指標
件產品,并得到如下統計表.該廠生產的產品在一年內所需的維護次數與指標![]() 有關,具體見下表.
有關,具體見下表.
質量指標 |
|
|
|
頻數 |
|
|
|
一年內所需維護次數 |
|
|
|
(1)以每個區間的中點值作為每組指標的代表,用上述樣本數據估計該廠產品的質量指標![]() 的平均值(保留兩位小數);
的平均值(保留兩位小數);
(2)用分層抽樣的方法從上述樣本中先抽取![]() 件產品,再從
件產品,再從![]() 件產品中隨機抽取
件產品中隨機抽取![]() 件產品,求這
件產品,求這![]() 件產品的指標
件產品的指標![]() 都在
都在![]() 內的概率;
內的概率;
(3)已知該廠產品的維護費用為![]() 元/次,工廠現推出一項服務:若消費者在購買該廠產品時每件多加
元/次,工廠現推出一項服務:若消費者在購買該廠產品時每件多加![]() 元,該產品即可一年內免費維護一次.將每件產品的購買支出和一年的維護支出之和稱為消費費用.假設這
元,該產品即可一年內免費維護一次.將每件產品的購買支出和一年的維護支出之和稱為消費費用.假設這![]() 件產品每件都購買該服務,或者每件都不購買該服務,就這兩種情況分別計算每件產品的平均消費費用,并以此為決策依據,判斷消費者在購買每件產品時是否值得購買這項維護服務?
件產品每件都購買該服務,或者每件都不購買該服務,就這兩種情況分別計算每件產品的平均消費費用,并以此為決策依據,判斷消費者在購買每件產品時是否值得購買這項維護服務?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某籃球隊甲、乙兩名運動員練習罰球,每人練習10組,每組罰球40個.命中個數的莖葉圖如圖,則下面結論中錯誤的一個是( )

A. 甲的極差是29 B. 甲的中位數是24
C. 甲罰球命中率比乙高 D. 乙的眾數是21
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】試研究,一個三角形能否同時具有以下兩個性質:(1)三邊是連續的三個自然數;(2)最大角是最小角的2倍.若能,請求出這個三角形的三邊以及最大角的余弦值;若不能,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,
,![]() 是橢圓
是橢圓![]() :
:![]() 的左右兩個焦點,過
的左右兩個焦點,過![]() 的直線與
的直線與![]() 交于
交于![]() ,
,![]() 兩點(
兩點(![]() 在第一象限),
在第一象限),![]() 的周長為8,
的周長為8,![]() 的離心率為
的離心率為![]() .
.
(1)求![]() 的方程;
的方程;
(2)設![]() ,
,![]() 為
為![]() 的左右頂點,直線
的左右頂點,直線![]() 的斜率為
的斜率為![]() ,
,![]() 的斜率為
的斜率為![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】平面直角坐標系xOy中,已知橢圓C:![]() 的離心率為
的離心率為![]() ,且點
,且點![]() 在橢圓C上.橢圓C的左頂點為A.
在橢圓C上.橢圓C的左頂點為A.
(1)求橢圓C的方程
(2)橢圓的右焦點且斜率為![]() 的直線與橢圓交于P,Q兩點,求三角形APQ的面積;
的直線與橢圓交于P,Q兩點,求三角形APQ的面積;
(3)過點A作直線與橢圓C交于另一點B.若直線![]() 交
交![]() 軸于點C,且
軸于點C,且![]() ,求直線
,求直線![]() 的斜率.
的斜率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com