
【題目】隨著醫(yī)院對看病掛號的改革,網(wǎng)上預(yù)約成為了當(dāng)前最熱門的就診方式,這解決了看病期間病人插隊以及醫(yī)生先治療熟悉病人等諸多問題;某醫(yī)院研究人員對其所在地區(qū)年齡在10~60歲間的![]() 位市民對網(wǎng)上預(yù)約掛號的了解情況作出調(diào)查,并將被調(diào)查的人員的年齡情況繪制成頻率分布直方圖,如下所示.
位市民對網(wǎng)上預(yù)約掛號的了解情況作出調(diào)查,并將被調(diào)查的人員的年齡情況繪制成頻率分布直方圖,如下所示.
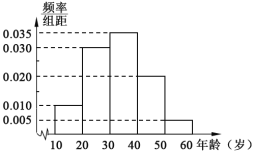
(1)若被調(diào)查的人員年齡在20~30歲間的市民有300人,求被調(diào)查人員的年齡在40歲以上(含40歲)的市民人數(shù);
(2)若按分層抽樣的方法從年齡在![]() 以及
以及![]() 內(nèi)的市民中隨機(jī)抽取10人,再從這10人中隨機(jī)抽取3人進(jìn)行調(diào)研,記隨機(jī)抽取的3人中,年齡在
內(nèi)的市民中隨機(jī)抽取10人,再從這10人中隨機(jī)抽取3人進(jìn)行調(diào)研,記隨機(jī)抽取的3人中,年齡在![]() 內(nèi)的人數(shù)為
內(nèi)的人數(shù)為![]() ,求
,求![]() 的分布列以及數(shù)學(xué)期望.
的分布列以及數(shù)學(xué)期望.

| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在某市高中某學(xué)科競賽中,某一個區(qū)4000名考生的參賽成績統(tǒng)計如圖所示.
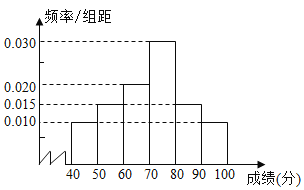
(1)求這4000名考生的競賽平均成績![]() (同一組中數(shù)據(jù)用該組區(qū)間中點(diǎn)作代表);
(同一組中數(shù)據(jù)用該組區(qū)間中點(diǎn)作代表);
(2)記70分以上為優(yōu)秀,70分及以下為合格,結(jié)合頻率分布直方圖完成下表,并判斷是否有99%的把握認(rèn)為該學(xué)科競賽成績與性別有關(guān)?
合格 | 優(yōu)秀 | 合計 | |
男生 | 720 |
|
|
女生 |
| 1020 |
|
合計 |
|
| 4000 |
附:
p(k2≥k0) | 0.010 | 0.005 | 0.001 |
k0 | 6.635 | 7.879 | 10.828 |
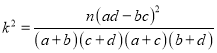 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在直三棱柱ABC﹣A1B1C1中,∠BAC=90°,AB=AC=AA1.

(1)求證:AB1⊥平面A1BC1;
(2)若D在B1C1上,滿足B1D=2DC1,求AD與平面A1BC1所成的角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】圓錐![]() (其中
(其中![]() 為頂點(diǎn),
為頂點(diǎn),![]() 為底面圓心)的側(cè)面積與底面積的比是
為底面圓心)的側(cè)面積與底面積的比是![]() ,則圓錐
,則圓錐![]() 與它外接球(即頂點(diǎn)在球面上且底面圓周也在球面上)的體積比為( )
與它外接球(即頂點(diǎn)在球面上且底面圓周也在球面上)的體積比為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為了調(diào)查國企員工對新個稅法的滿意程度,研究人員在![]() 地各個國企中隨機(jī)抽取了1000名員工進(jìn)行調(diào)查,并將滿意程度以分?jǐn)?shù)的形式統(tǒng)計成如下的頻率分布表,其中
地各個國企中隨機(jī)抽取了1000名員工進(jìn)行調(diào)查,并將滿意程度以分?jǐn)?shù)的形式統(tǒng)計成如下的頻率分布表,其中![]() .(計算結(jié)果保留兩位小數(shù))
.(計算結(jié)果保留兩位小數(shù))
分?jǐn)?shù) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
頻率 | 0.08 |
| 0.35 | 0.27 |
|
(1)試估計被調(diào)查的員工的滿意程度的中位數(shù);
(2)若把每組的組中值作為該組的滿意程度,試估計被調(diào)查的員工的滿意程度的平均數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】中央政府為了對應(yīng)因人口老齡化而造成的勞動力短缺等問題,擬定出臺“延遲退休年齡政策”,為了了解人們對“延遲退休年齡政策”的態(tài)度,責(zé)成人社部進(jìn)行調(diào)研,人社部從網(wǎng)上年齡在15~65的人群中隨機(jī)調(diào)查50人,調(diào)查數(shù)據(jù)的頻率分布直方圖和支持“延遲退休”的人數(shù)與年齡的統(tǒng)計結(jié)果如下:
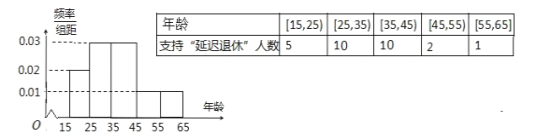
(1)由以上統(tǒng)計數(shù)據(jù)填下面2×2列聯(lián)表,并問是否有90%的把握認(rèn)為以45歲為分界點(diǎn)對“延遲退休年齡政策”的支持度有差異:
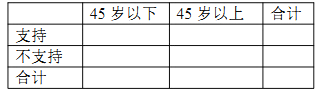
(2)若從年齡在![]() 的被調(diào)查人中隨機(jī)選取兩人進(jìn)行調(diào)查,求選中的2人中恰有1人支持“延遲退休”的概率.
的被調(diào)查人中隨機(jī)選取兩人進(jìn)行調(diào)查,求選中的2人中恰有1人支持“延遲退休”的概率.
參考數(shù)據(jù):
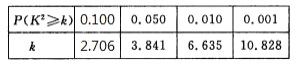
![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() ,
,![]() ,其中
,其中![]() ,函數(shù)
,函數(shù)![]() 與
與![]() 關(guān)于直線
關(guān)于直線![]() 對稱.
對稱.
(1)若函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上遞增,求a的取值范圍;
上遞增,求a的取值范圍;
(2)證明:![]() ;
;
(3)設(shè)![]() ,其中
,其中![]() 恒成立,求滿足條件的最小正整數(shù)b的值.
恒成立,求滿足條件的最小正整數(shù)b的值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com