
【題目】已知函數f(x)(x∈R)滿足f(x)=f(2-x),且對任意的x1,x2∈(-∞,1](x1≠x2)有(x1-x2)(f(x1)-f(x2))<0.則( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】因金融危機,某公司的出口額下降,為此有關專家提出兩種促進出口的方案,每種方案都需要分兩年實施。若實施方案一,預計第一年可以使出口額恢復到危機前的![]() 倍、
倍、![]() 倍、
倍、![]() 倍的概率分別為
倍的概率分別為![]() 、
、![]() 、
、![]() ;第二年可以使出口額為第一年的
;第二年可以使出口額為第一年的![]() 倍、
倍、![]() 倍的概率分別為
倍的概率分別為![]() 、
、![]() 。若實施方案二,預計第一年可以使出口額恢復到危機前的
。若實施方案二,預計第一年可以使出口額恢復到危機前的![]() 倍、
倍、![]() 倍、
倍、![]() 倍的概率分別為
倍的概率分別為![]() 、
、![]() 、
、![]() ;第二年可以使出口額為第一年的
;第二年可以使出口額為第一年的![]() 倍、
倍、![]() 倍的概率分別為
倍的概率分別為![]() 、
、![]() 。實施每種方案第一年與第二年相互獨立。令
。實施每種方案第一年與第二年相互獨立。令![]() 表示方案
表示方案![]() 實施兩年后出口額達到危機前的倍數。
實施兩年后出口額達到危機前的倍數。
(1)寫出![]() 的分布列;
的分布列;
(2)實施哪種方案,兩年后出口額超過危機前出口額的概率更大?
(3)不管哪種方案,如果實施兩年后出口額達不到、恰好達到、超過危機前出口額,預計利潤分別為![]() 萬元、
萬元、![]() 萬元、
萬元、![]() 萬元,問實施哪種方案的平均利潤更大?
萬元,問實施哪種方案的平均利潤更大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ln x-a(x-1),g(x)=ex.
(1)求函數f(x)的單調區間;
(2)若函數h(x)=f(x+1)+g(x),當x>0時,h(x)>1恒成立,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知0<a<b,且a+b=1,則下列不等式中正確的是( )
A.log2a>0
B.2a﹣b< ![]()
C.log2a+log2b<﹣2
D.2( ![]() +
+ ![]() )<
)< ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法正確的是( )
A. 某廠一批產品的次品率為![]() ,則任意抽取其中10件產品一定會發現一件次品
,則任意抽取其中10件產品一定會發現一件次品
B. 擲一枚硬幣,連續出現5次正面向上,第六次出現反面向上的概率與正面向上的概率仍然都為0.5
C. 某醫院治療一種疾病的治愈率為10%,那么前9個病人都沒有治愈,第10個人就一定能治愈
D. 氣象部門預報明天下雨的概率是90%,說明明天該地區90%的地方要下雨,其余10%的地方不會下雨
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下表是最近十屆奧運會的年份、屆別、主辦國,以及主辦國在上屆獲得的金牌數、當屆
獲得的金牌數的統計數據:
年份 | 1972 | 1976 | 1980 | 1984 | 1988 | 1992 | 1996 | 2000 | 2004 | 2008 |
屆別 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
主辦國家 | 聯邦 德國 | 加拿大 | 蘇聯 | 美國 | 韓國 | 西班牙 | 美國 | 澳大 利亞 | 希臘 | 中國 |
上屆金牌數 | 5 | 0 | 49 | 未參加 | 6 | 1 | 37 | 9 | 4 | 32 |
當界金牌數 | 13 | 0 | 80 | 83 | 12 | 13 | 44 | 16 | 6 | 51 |
某體育愛好組織,利用上表研究所獲金牌數與主辦奧運會之間的關系,
(1)求出主辦國在上屆所獲金牌數(設為![]() )與在當屆所獲金牌數(設為
)與在當屆所獲金牌數(設為![]() )之間的線性回歸方程
)之間的線性回歸方程
![]() 其中
其中![]()
(2)在2008年第29屆北京奧運會上日本獲得9塊金牌,則據此線性回歸方程估計在2020 年第 32 屆東
京奧運會上日本將獲得的金牌數為(所有金牌數精確到整數)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐PABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中點.
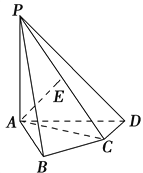
(1)證明:AE⊥平面PCD;
(2)求二面角A-PD-C的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校為準備參加市運動會,對本校高一、高二兩個田徑隊中30名跳高運動員進行了測試,并用莖葉圖表示出本次測試30人的跳高成績(單位:cm).跳高成績在175cm以上(包括175cm)定義為“合格”,成績在175cm以下定義為“不合格”.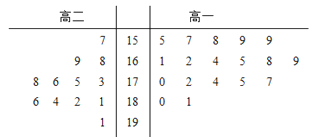
(1)如果從所有運動員中用分層抽樣抽取“合格”與“不合格”的人數共10人,問就抽取“合格”人數是多少?
(2)若從所有“合格”運動員中選取2名,用X表示所選運動員來自高一隊的人數,試寫出X的分布圖,并求X的數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com