
【題目】已知函數f(x)=3x , g(x)=|x+a|﹣3,其中a∈R. (Ⅰ)若函數h(x)=f[g(x)]的圖象關于直線x=2對稱,求a的值;
(Ⅱ)給出函數y=g[f(x)]的零點個數,并說明理由.
【答案】解:(Ⅰ)函數h(x)=f[g(x)]=3|x+a|﹣3的圖象關于直線x=2對稱,則h(4﹣x)=h(x)|x+a|=|4﹣x+a|恒成立a=﹣2;
(Ⅱ)函數y=g[f(x)]=|3x+a|﹣3的零點個數,就是函數G(x)=|3x+a|與y=3的交點,
①當0≤a<3時,G(x)=|3x+a|=3x+a與y=3的交點只有一個,即函數y=g[f(x)]的零點個數為1個(如圖1);
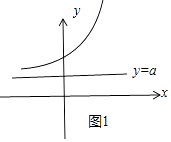
②當a≥3時,G(x)=|3x+a|=3x+a與y=3沒有交點,即函數y=g[f(x)]的零點個數為0個(如圖1);
③﹣3≤a<0時,G(x)=|3x+a|與y=3的交點只有1個(如圖2);
④當a<﹣3時,G(x)=|3x+a|與y=3的交點有2個(如圖2);

【解析】(Ⅰ)函數h(x)=f[g(x)]=3|x+a|﹣3的圖象關于直線x=2對稱,則h(4﹣x)=h(x)|x+a|=|4﹣x+a|恒成立a=﹣2;(Ⅱ)函數y=g[f(x)]=|3x+a|﹣3的零點個數,就是函數G(x)=|3x+a|與y=3的交點,
分①當0≤a<3時;②當a≥3時;③﹣3≤a<0時;④當a<﹣3時,畫出圖象判斷個數.
【考點精析】解答此題的關鍵在于理解利用導數研究函數的單調性的相關知識,掌握一般的,函數的單調性與其導數的正負有如下關系: 在某個區間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞增;(2)如果
在這個區間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞減.
在這個區間單調遞減.


 開心蛙狀元作業系列答案
開心蛙狀元作業系列答案 課時掌控隨堂練習系列答案
課時掌控隨堂練習系列答案 一課一練一本通系列答案
一課一練一本通系列答案 浙江之星學業水平測試系列答案
浙江之星學業水平測試系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() .
.
(1)求f(f( ![]() ));
));
(2)若x0滿足f(f(x0))=x0 , 且f(x0)≠x0 , 則稱x0為f(x)的二階不動點,求函數f(x)的二階不動點的個數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】春節是旅游消費旺季,某大型商場通過對春節前后20天的調查,得到部分日經濟收入Q與這20天中的第x天(x∈N+)的部分數據如表:
天數x(天) | 3 | 5 | 7 | 9 | 11 | 13 | 15 |
日經濟收入Q(萬元) | 154 | 180 | 198 | 208 | 210 | 204 | 190 |
(1)根據表中數據,結合函數圖象的性質,從下列函數模型中選取一個最恰當的函數模型描述Q與x的變化關系,只需說明理由,不用證明. ①Q=ax+b,②Q=﹣x2+ax+b,③Q=ax+b,④Q=b+logax.
(2)結合表中的數據,根據你選擇的函數模型,求出該函數的解析式,并確定日經濟收入最高的是第幾天;并求出這個最高值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,角A,B,C對應的邊分別是a,b,c,已知cos2A﹣3cos(B+C)=1. (Ⅰ)求角A的大小;
(Ⅱ)若△ABC的面積S=5 ![]() ,b=5,求sinBsinC的值.
,b=5,求sinBsinC的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知△ABC的三個內角A,B,C的對邊分別是a,b,c,且bcosC=(2a﹣c)cosB.
(1)求角B.
(2)若 ![]() ,△ABC的周長為
,△ABC的周長為 ![]() ,求△ABC的面積.
,求△ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,PD⊥平面ABCD,AB∥CD,∠ADC=90°,PD=AD=AB=1,DC=2. 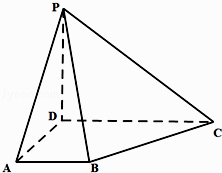
(1)求證:BC⊥平面PBD;
(2)求二面角A﹣PB﹣C的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示的多面體,它的正視圖為直角三角形,側視圖為正三角形,俯視圖為正方形(尺寸如圖所示),E為VB的中點. 
(1)求證:VD∥平面EAC;
(2)求二面角A﹣VB﹣D的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,F1、F2是雙曲線 ![]() =1(a>0,b>0)的左、右焦點,過F1的直線l與雙曲線的左右兩支分別交于點A、B.若△ABF2為等邊三角形,則雙曲線的離心率為( )
=1(a>0,b>0)的左、右焦點,過F1的直線l與雙曲線的左右兩支分別交于點A、B.若△ABF2為等邊三角形,則雙曲線的離心率為( ) 
A.4
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com