【題目】已知函數
， 
.
（1）當
時，求函數
的最大值；
（2）若
，且對任意的
， 
恒成立，求實數
的取值范圍.
【答案】(1)0；(2) 
.
【解析】試題分析：（1）求出函數的導數，得到函數的單調區間，求出函數的最大值即可；
（2）令（x）=f（x）+1，根據函數的單調性分別求出φ（x）的最小值和g（x）的最大值，得到關于m的不等式，解出即可．
試題解析：
（1）函數
的定義域為
，
當
時， 
，
∴當
時， 
，函數
在
上單調遞增，
∴當
時， 
，函數
在
上單調遞減，
∴
.
（2）令
，因為“對任意的
， 
恒成立”，
所以對任意的
， 
成立，由于
，
當
時，對
有
，從而函數
在
上單調遞增，
所以
，
，
當
時， 
， 
時， 
，顯然不滿足
，
當
時，令
得
， 
，
①當
，即
時，在
上
，所以
在
上單調遞增，所以
，只需
，得
，所以
.
②當
，即
時，在
上
， 
單調遞增，在
上
， 
單調遞減，所以
，只需
，得
，所以
.
③當
，即
時，顯然在
上
， 
單調遞增，所以
， 
不成立.
綜上所述， 
的取值范圍是
.
科目：高中數學 來源： 題型：
【題目】已知f（x）=ax﹣lnx，x∈（0，e]，其中e是自然常數，a∈R．
（1）當a=1時，求f（x）的單調區間和極值；
（2）是否存在實數a，使f（x）的最小值是3，若存在，求出a的值；若不存在，說明理由．
（3）證明：（1﹣ 
）（ 
）（ 
﹣ 
）…（ 
﹣ 
）＜e3（3﹣n） ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】一個勻速旋轉的摩天輪每12分鐘轉一周，最低點距地面2米，最高點距地面18米，P是摩天輪輪周上一定點，從P在最低點時開始計時，則14分鐘后P點距地面的高度是米．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某正弦交流電的電壓v（單位V）隨時間t（單位：s）變化的函數關系是v=120 
sin（100πt﹣ 
），t∈[0，+∞）．
（1）求該正弦交流電電壓v的周期、頻率、振幅；
（2）若加在霓虹燈管兩端電壓大于84V時燈管才發光，求在半個周期內霓虹燈管點亮的時間？（ 取 ≈1.4）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了解學生寒假期間學習情況，學校對某班男、女學生學習時間進行調查，學習時間按整小時統計，調查結果繪成折線圖如下：
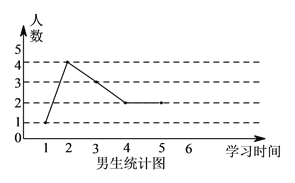
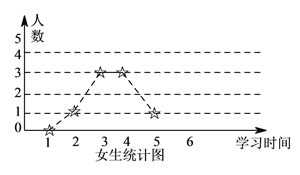
（I）已知該校有
名學生，試估計全校學生中，每天學習不足
小時的人數．
（II）若從學習時間不少于
小時的學生中選取
人，設選到的男生人數為
，求隨機變量
的分布列．
（III）試比較男生學習時間的方差
與女生學習時間方差
的大小．（只需寫出結論）．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設
， 
是橢圓
上的兩點，橢圓的離心率為
，短軸長為2，已知向量
， 
，且
， 
為坐標原點.
（1）若直線
過橢圓的焦點
，（ 
為半焦距），求直線
的斜率
的值；
（2）試問： 
的面積是否為定值？如果是，請給予證明；如果不是，請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
