
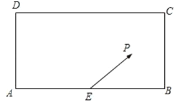
【題目】某校興趣小組在如圖所示的矩形區域![]() 內舉行機器人攔截挑戰賽,在
內舉行機器人攔截挑戰賽,在![]() 處按
處按![]() 方向釋放機器人甲,同時在
方向釋放機器人甲,同時在![]() 處按某方向釋放機器人乙,設機器人乙在
處按某方向釋放機器人乙,設機器人乙在![]() 處成功攔截機器人甲.若點
處成功攔截機器人甲.若點![]() 在矩形區域
在矩形區域![]() 內(包含邊界),則挑戰成功,否則挑戰失敗.已知
內(包含邊界),則挑戰成功,否則挑戰失敗.已知![]() 米,
米,![]() 為
為![]() 中點,機器人乙的速度是機器人甲的速度的2倍,比賽中兩機器人均按勻速直線運動方式行進,記
中點,機器人乙的速度是機器人甲的速度的2倍,比賽中兩機器人均按勻速直線運動方式行進,記![]() 與
與![]() 的夾角為
的夾角為![]() .
.
(1)若![]() ,
,![]() 足夠長,則如何設置機器人乙的釋放角度才能挑戰成功?(結果精確到
足夠長,則如何設置機器人乙的釋放角度才能挑戰成功?(結果精確到![]() );
);
(2)如何設計矩形區域![]() 的寬
的寬![]() 的長度,才能確保無論
的長度,才能確保無論![]() 的值為多少,總可以通過設置機器人乙的釋放角度使機器人乙在矩形區域
的值為多少,總可以通過設置機器人乙的釋放角度使機器人乙在矩形區域![]() 內成功攔截機器人甲?
內成功攔截機器人甲?
 優生樂園系列答案
優生樂園系列答案 新編小學單元自測題系列答案
新編小學單元自測題系列答案科目:高中數學 來源: 題型:
【題目】2019年6月25日,《固體廢物污染環境防治法(修訂草案)》初次提請全國人大常委會審議,草案對“生活垃圾污染環境的防治”進行了專章規定.草案提出,國家推行生活垃圾分類制度.為了了解人民群眾對垃圾分類的認識,某市環保部門對該市市民進行了一次垃圾分類網絡知識問卷調查,每一位市民僅有一次參加機會,通過隨機抽樣,得到參加問卷調查的1000人的得分(滿分:100分)數據,統計結果如表所示:
得分 |
|
|
|
|
|
|
|
頻數 | 25 | 150 | 200 | 250 | 225 | 100 | 50 |
(1)由頻數分布表可以認為,此次問卷調查的得分![]() 服從正態分布
服從正態分布![]() ,
,![]() 近似為這1000人得分的平均值(同一組數據用該組區間的中點值作為代表),請利用正態分布的知識求
近似為這1000人得分的平均值(同一組數據用該組區間的中點值作為代表),請利用正態分布的知識求![]() ;
;
(2)在(1)的條件下,市環保部門為此次參加問卷調查的市民制定如下獎勵方案:
①得分不低于![]() “的可以獲贈2次隨機話費,得分低于
“的可以獲贈2次隨機話費,得分低于![]() 的可以獲贈1次隨機話費;
的可以獲贈1次隨機話費;
②每次獲贈的隨機話費和對應的概率為:
獲贈的隨機話費(單位:元) | 20 | 40 |
概率 |
|
|
現市民小王要參加此次問卷調查,記![]() (單位:元)為該市民參加問卷調查獲贈的話費,求
(單位:元)為該市民參加問卷調查獲贈的話費,求![]() 的分布列及數學期望.
的分布列及數學期望.
附:①![]() ;②若
;②若![]() ,則
,則![]() ,
,![]() ,
,![]() ,
,
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知 m、n 是兩條不同的直線,α、β、γ是三個不同的平面,下列命題中正確的是( )
A.若α⊥β , β⊥γ ,則α∥γ
B.若 ![]() ,
, ![]() , m∥n ,則α∥β
, m∥n ,則α∥β
C.若 m、n 是異面直線, ![]() , m∥β ,
, m∥β , ![]() , n∥α ,則α∥β
, n∥α ,則α∥β
D.平面α內有不共線的三點到平面 β的距離相等,則α∥β
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個調查學生記憶力的研究團隊從某中學隨機挑選100名學生進行記憶測試,通過講解100個陌生單詞后,相隔十分鐘進行聽寫測試,間隔時間![]() (分鐘)和答對人數
(分鐘)和答對人數![]() 的統計表格如下:
的統計表格如下:
時間 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
答對人數 | 98 | 70 | 52 | 36 | 30 | 20 | 15 | 11 | 5 | 5 |
| 1.99 | 1.85 | 1.72 | 1.56 | 1.48 | 1.30 | 1.18 | 1.04 | 0.7 | 0.7 |
時間![]() 與答對人數
與答對人數![]() 的散點圖如圖:
的散點圖如圖:
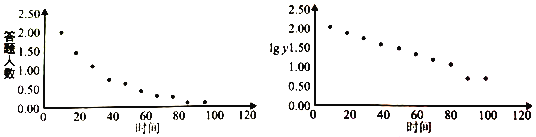
附:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,對于一組數據
,對于一組數據![]() ,
,![]() ,……,
,……,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為: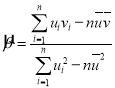 ,
,![]() .請根據表格數據回答下列問題:
.請根據表格數據回答下列問題:
(1)根據散點圖判斷,![]() 與
與![]() ,哪個更適宣作為線性回歸類型?(給出判斷即可,不必說明理由)
,哪個更適宣作為線性回歸類型?(給出判斷即可,不必說明理由)
(2)根據(1)的判斷結果,建立![]() 與
與![]() 的回歸方程;(數據保留3位有效數字)
的回歸方程;(數據保留3位有效數字)
(3)根據(2)請估算要想記住![]() 的內容,至多間隔多少分鐘重新記憶一遍.(參考數據:
的內容,至多間隔多少分鐘重新記憶一遍.(參考數據:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》中有如下問題:今有蒲生一日,長四尺,莞生一日,長一尺.蒲生日自半,莞生日自倍.意思是:今有蒲第一天長高四尺,莞第一天長高一尺,以后蒲每天長高前一天的一半,莞每天長高前一天的兩倍.請問第幾天,莞的長度是蒲的長度的4倍( )
A.4天B.5天C.6天D.7天
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若定義域均為D的三個函數f(x),g(x),h(x)滿足條件:對任意x∈D,點(x,g(x)與點(x,h(x)都關于點(x,f(x)對稱,則稱h(x)是g(x)關于f(x)的“對稱函數”.已知g(x)=![]() ,f(x)=2x+b,h(x)是g(x)關于f(x)的“對稱函數”,且h(x)≥g(x)恒成立,則實數b的取值范圍是_____.
,f(x)=2x+b,h(x)是g(x)關于f(x)的“對稱函數”,且h(x)≥g(x)恒成立,則實數b的取值范圍是_____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“干支紀年法”是中國歷法上自古以來就一直使用的紀年方法,甲、乙、丙、丁、戊、己、庚、辛、壬、癸被稱為“十天干”,子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥叫做“十二地支”.“天干”以“甲”字開始,“地支”以“子”字開始,兩者按照干支順序相配,構成了“干支紀年法”,其相配順序為:甲子、乙丑、丙寅![]() 癸酉、甲戌、乙亥、丙子
癸酉、甲戌、乙亥、丙子![]() 癸未、甲申、乙酉、丙戌
癸未、甲申、乙酉、丙戌![]() 癸巳
癸巳![]() 癸亥,60為一個周期,周而復始,循環記錄.按照“干支紀年法”,中華人民共和國成立的那年為己丑年,則2013年為( )
癸亥,60為一個周期,周而復始,循環記錄.按照“干支紀年法”,中華人民共和國成立的那年為己丑年,則2013年為( )
A.甲巳年B.壬辰年C.癸巳年D.辛卯年
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() 的離心率
的離心率![]() ,橢圓C上的點到其左焦點的最大距離為
,橢圓C上的點到其左焦點的最大距離為![]() .
.
(Ⅰ)求橢圓C的方程;
(Ⅱ)過點A![]() 作直線
作直線![]() 與橢圓相交于點B,則
與橢圓相交于點B,則![]() 軸上是否存在點P,使得線段
軸上是否存在點P,使得線段![]() ,且
,且![]() ?若存在,求出點P坐標;否則請說明理由.
?若存在,求出點P坐標;否則請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com