
【題目】已知函數![]() .
.
(Ⅰ)當![]() 時,證明:
時,證明: ![]() 在定義域上為減函數;
在定義域上為減函數;
(Ⅱ)若![]() .討論函數
.討論函數![]() 的零點情況.
的零點情況.
【答案】(1)見解析(2)當![]() 時,函數
時,函數![]() 無零點;當
無零點;當![]() 或
或![]() 時,函數
時,函數![]() 有一個零點;當
有一個零點;當![]() 時,函數
時,函數![]() 有兩個零點.
有兩個零點.
【解析】試題分析:(Ⅰ)當![]() 時,對函數求導,利用導數與函數單調性的關系,可證明函數在定義域上為減函數;(Ⅱ)
時,對函數求導,利用導數與函數單調性的關系,可證明函數在定義域上為減函數;(Ⅱ) ![]() 的根情況,方程化簡為
的根情況,方程化簡為![]() ,構造函數
,構造函數![]() ,利用導數判斷這個函數的取值情況,與
,利用導數判斷這個函數的取值情況,與![]() 結合可得,函數
結合可得,函數![]() 的零點情況.
的零點情況.
試題解析:(Ⅰ)由題意可知函數![]() 的定義域為
的定義域為![]() .
.
![]() ,令
,令![]() ,則
,則![]() ,
,
當![]() 時,
時, ![]() ;當
;當![]() 時,
時, ![]() ,所以
,所以![]() ,
,
即![]() ,所以
,所以![]() ,所以
,所以![]() 在定義域上為減函數.
在定義域上為減函數.
(Ⅱ)![]() 的零點情況,即方程
的零點情況,即方程![]() 的根情況,
的根情況,
因為![]() ,所以方程可化為
,所以方程可化為![]() ,
,
令![]() ,則
,則![]() ,令
,令![]() ,可得
,可得![]() ,
,
當![]() 時,
時, ![]() ,
,
當![]() 時,
時, ![]() ,所以
,所以![]() ,
,
且當![]() 時,
時, ![]() ;當
;當![]() 時,
時, ![]() ,
,
所以![]() 的圖像大致如圖所示,
的圖像大致如圖所示,

結合圖像可知,當![]() 時,方程
時,方程![]() 沒有根;
沒有根;
當![]() 或
或![]() 時,方程
時,方程![]() 有一個根;
有一個根;
當![]() 時,方程
時,方程![]() 有兩個根.
有兩個根.
所以當![]() 時,函數
時,函數![]() 無零點;當
無零點;當![]() 或
或![]() 時,函數
時,函數![]() 有一個零點;當
有一個零點;當![]() 時,函數
時,函數![]() 有兩個零點.
有兩個零點.


 全優沖刺100分系列答案
全優沖刺100分系列答案 英才點津系列答案
英才點津系列答案 紅果子三級測試卷系列答案
紅果子三級測試卷系列答案科目:高中數學 來源: 題型:
【題目】在多面體ABCDEF中,底面ABCD是梯形,四邊形ADEF是正方形,AB∥DC,AB=AD=1,CD=2,AC=EC=![]() 。
。
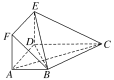
(1)求證:平面EBC⊥平面EBD;
(2)設M為線段EC上一點,且3EM=EC,試問在線段BC上是否存在一點T,使得MT∥平面BDE,若存在,試指出點T的位置;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com