【題目】為了適應新高考改革，某校組織了一次新高考質量測評（總分100分），在成績統計分析中，抽取12名學生的成績以莖葉圖形式表示如圖，學校規定測試成績低于87分的為“未達標”，分數不低于87分的為“達標”.
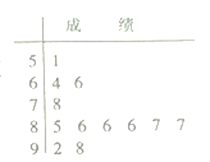
（1）求這組數據的眾數和平均數；
（2）在這12名學生中從測試成績介于80~90之間的學生中任選2人，求至少有1人“達標”的概率.
【答案】（1）86,80.5；（2）
.
【解析】
（1）找出莖葉圖中出現次數最多的數為眾數，根據平均數公式，即可求得平均數；
（2）在被抽取的學生中，有2個“達標”學生，4個“未達標”學生，按達標和不達標兩類編號，列出從6人中任取2人的所有情況，統計出滿足條件的基本事件的個數，根據古典概型的概率公式，即可求解.
(1)這組數據的眾數為86；
平均數為
.
(2)在被抽取的學生中，有2個“達標”學生，4個“未達標”學生，
將“達標”學生編號為
，
，“未達標”學生編號為
，
，
，
，
則從6人中任取2人,有以下情況：
，
，
，
，
，
，
，
，
，
，
，
，
，
，
.共15種.
其中符合條件的為，，，，，，
，，，共9種.
故至少有1人“達標”的概率
.
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】已知函數
在
處的切線
與直線
平行.
（1）求實數
的值；
（2）若函數
在
上恰有兩個零點，求實數
的取值范圍.
（3）記函數
，設
是函數
的兩個極值點，若
，且
恒成立，求實數
的最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】“科技引領，布局未來”科技研發是企業發展的驅動力量.2007年至2018年，某企業連續12年累計研發投入達4100億元，我們將研發投入與經營收入的比值記為研發投入占營收比．這12年間的研發投入（單位：十億元）用圖中的條形圖表示，研發投入占營收比用圖中的折線圖表示．
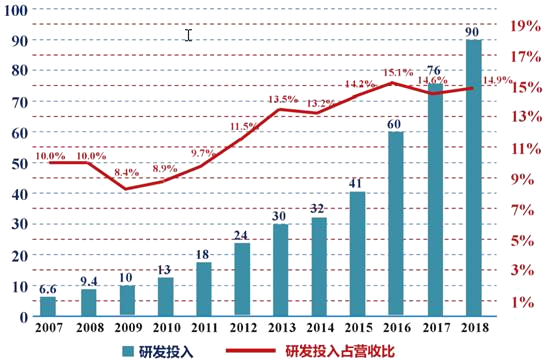
根據折線圖和條形圖，下列結論錯誤的是（ ）
A. 2012﹣2013 年研發投入占營收比增量相比 2017﹣2018 年增量大
B. 該企業連續 12 年研發投入逐年增加
C. 2015﹣2016 年研發投入增值最大
D. 該企業連續 12 年研發投入占營收比逐年增加
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
