
���}Ŀ����D��ʾ����ֱ������![]() �У�ƽ��
�У�ƽ��![]() ��(c��)��
��(c��)��![]() ����
����![]() ��
��

��1�����C��![]() ��
��
��2����ֱ��![]() �cƽ��
�cƽ��![]() ���ɽǵ�����ֵ��
���ɽǵ�����ֵ��![]() �����J�����
�����J�����![]() �Ĵ�С��
�Ĵ�С��
���𰸡���1��Ҋ��������2��![]() ��
��
��������ԇ�}��������1��ȡ![]() �����c(di��n)
�����c(di��n)![]() ���B��
���B��![]() ������֪�l���ƌ�(d��o)��
������֪�l���ƌ�(d��o)��![]() ƽ��
ƽ��![]() ���Ķ��õ�
���Ķ��õ�![]() ���ɾ��洹ֱ��
���ɾ��洹ֱ��![]() ���ɴ˿��C��
���ɴ˿��C��![]() ����2���B��
����2���B��![]() ���ɣ�1����֪
���ɣ�1����֪![]() ƽ��
ƽ��![]() ������֪�l���õ�
������֪�l���õ�![]() ����ֱ��
����ֱ��![]() �cƽ��
�cƽ��![]() ���ɵĽǣ�
���ɵĽǣ�![]() �������
�������![]() ��һ��(g��)ƽ��ǣ�����������ǵĴ�С��
��һ��(g��)ƽ��ǣ�����������ǵĴ�С��
ԇ�}��������1����D��ȡ![]() �����c(di��n)
�����c(di��n)![]() ���B��
���B��![]() ,��?y��n)?/span>
,��?y��n)?/span>![]() ,����
,����![]() ,
,
��ƽ��![]() ��(c��)��
��(c��)��![]() ,��ƽ��
,��ƽ��![]() ��(c��)��
��(c��)��![]() ��
��![]() ƽ��
ƽ��![]() ��
��
��![]() ƽ��
ƽ��![]() ������
������![]() ��
��
��?y��n)������?/span>![]() ��ֱ������,�t
��ֱ������,�t![]() ����
����![]() ������?y��n)?/span>
������?y��n)?/span>![]() ƽ��
ƽ��![]() ,
,
����![]() ����
����![]() ������
������![]() ��(c��)��
��(c��)��![]() ��
��
��![]() ��(c��)��
��(c��)��![]() ����
����![]() ��
��

��2���B��![]() ���ɣ�1����֪
���ɣ�1����֪![]() ƽ��
ƽ��![]() ,�t
,�t![]() ��
��![]() ��ƽ��
��ƽ��![]() ��(n��i)����Ӱ��
��(n��i)����Ӱ��
����![]() ����ֱ��
����ֱ��![]() �cƽ��
�cƽ��![]() ���ɵĽǣ�
���ɵĽǣ�
��?y��n)�ֱ��![]() �cƽ��
�cƽ��![]() ���ɵĽǵ�����ֵ��
���ɵĽǵ�����ֵ��![]() ,����
,����![]() ,
,
�ڵ���ֱ��![]() �У�
��![]() ���c(di��n)
���c(di��n)![]() ��
��![]() ���c(di��n)������
���c(di��n)������![]() ��
��
��![]() ,����
,����![]() ���^�c(di��n)
���^�c(di��n)![]() ��
��![]() ���c(di��n)
���c(di��n)![]() ���B��
���B��![]() ,
,
�ɣ�1��֪![]() ƽ��
ƽ��![]() ,�t
,�t![]() ,��
,��![]() ,����
,����![]() ƽ��
ƽ��![]() ,
,
����![]() ,����
,����![]() �������
�������![]() ��һ��(g��)ƽ��ǣ���ֱ��
��һ��(g��)ƽ��ǣ���ֱ��![]() �У�
��![]() ����
����![]() ,
,
����![]() ������?y��n)����?/span>
������?y��n)����?/span>![]() ���J�����,
���J�����,
����![]() �����J�����
�����J�����![]() �Ĵ�С��
�Ĵ�С��![]() ��
��



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]()
![]() ��
��![]() �φ��{(di��o)�f��,
�φ��{(di��o)�f��,
(1)������(sh��)![]() �Ќ�(sh��)��(sh��)���c(di��n)����M��l���Č�(sh��)��(sh��)
�Ќ�(sh��)��(sh��)���c(di��n)����M��l���Č�(sh��)��(sh��)![]() �ļ���
�ļ���![]() ��
��
(2)��(du��)�������![]() �r(sh��)������ʽ
�r(sh��)������ʽ![]() ���������
���������![]() ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��ij�����N������������ij֪��Ʒ�Ƶ�������(sh��)�W(xu��)��Ԫ��,�����ȔM���ăr(ji��)���M(j��n)��![]() ��ԇ�N��ÿ�N���r(ji��)ԇ�N
��ԇ�N��ÿ�N���r(ji��)ԇ�N![]() ��,�õ�����(sh��)��(j��):
��,�õ�����(sh��)��(j��):
�r(ji��) |
|
|
|
|
|
�N�� |
|
|
|
|
|
��1����ԇ�N![]() ����N���ķ����
����N���ķ����![]() ��(du��)
��(du��)![]() �Ļؚwֱ�����̣�
�Ļؚwֱ�����̣�
��2���A(y��)Ӌ(j��)�����N���У��N���c�r(ji��)������1���еĻؚw���̣���֪ÿ?j��)?c��)��Ԫ���ijɱ���![]() Ԫ,
Ԫ,
���˫@���������(r��n),ԓ��Ԫ���Ćr(ji��)��(y��ng)�������Ԫ��
��:  ,
, ![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���±��ṩ��ij��˾���g(sh��)����(j��)�����a(ch��n)![]() �a(ch��n)Ʒ�^����ӛ䛵Įa(ch��n)��
�a(ch��n)Ʒ�^����ӛ䛵Įa(ch��n)��![]() �������c����(y��ng)�ijɱ�
�������c����(y��ng)�ijɱ�![]() ���fԪ���ĎM��(du��)�Ք�(sh��)��(j��)��
���fԪ���ĎM��(du��)�Ք�(sh��)��(j��)��

��1��Ո(q��ng)�����ϱ픵(sh��)��(j��)��ɢ�c(di��n)�D��

��2��Ո(q��ng)����(j��)�ϱ��ṩ�Ĕ�(sh��)��(j��)������С���˷����![]() ��(du��)
��(du��)![]() �Ļؚwֱ�����̣�
�Ļؚwֱ�����̣�
��3����֪ԓ��˾���g(sh��)����(j��)ǰ���a(ch��n)100��![]() �a(ch��n)Ʒ�ijɱ���90�fԪ.ԇ����(j��)��2������Ļؚwֱ�����̣��A(y��)�y(c��)���g(sh��)����(j��)�����a(ch��n)100��
�a(ch��n)Ʒ�ijɱ���90�fԪ.ԇ����(j��)��2������Ļؚwֱ�����̣��A(y��)�y(c��)���g(sh��)����(j��)�����a(ch��n)100��![]() �a(ch��n)Ʒ�ijɱ��ȼ��g(sh��)����(j��)ǰ�s���Ͷ����fԪ��
�a(ch��n)Ʒ�ijɱ��ȼ��g(sh��)����(j��)ǰ�s���Ͷ����fԪ��
������  ��
�� ![]() ������
������![]() ��ӱ�ƽ��ֵ��
��ӱ�ƽ��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D��ʾ���������wABCD-A1B1C1D�У�S��B1D1�����c(di��n)��E��F��G�քe��BC��CD��SC�����c(di��n)�����C��
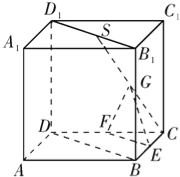
��1��ֱ��EG��ƽ��BDD1B1��
��2��ƽ��EFG��ƽ��BDD1B1��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����ֱ֪��l��![]() �c�AO��
�c�AO��![]() �ཻ��A��B�ɂ�(g��)��ͬ���c(di��n)����A
�ཻ��A��B�ɂ�(g��)��ͬ���c(di��n)����A![]() ��B
��B![]() .
.
��1����(d��ng)![]() ��e���r(sh��)����m��ȡֵ�������
��e���r(sh��)����m��ȡֵ�������![]() ���L(zh��ng)����
���L(zh��ng)����
��2���Д�![]() �Ƿ�鶨ֵ�����ǣ������ֵ�Ĵ�С�������ǣ��f��������
�Ƿ�鶨ֵ�����ǣ������ֵ�Ĵ�С�������ǣ��f��������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ�����˽�������όW(xu��)ʹ���֙C(j��)��r���{(di��o)�����M(j��n)�������µ��S�C(j��)�{(di��o)�飺�{(di��o)�������{(di��o)��������ɂ�(g��)���}����1����ČW(xu��)̖(h��o)���攵(sh��)���2�����όW(xu��)�r(sh��)�Ƿ�(j��ng)�����֙C(j��)��Ҫ���{(di��o)���߱���(du��)���{(di��o)���ˆT���SһöӲ�ţ�������F(xi��n)���棬�ͻش��һ���}����t�ͻش�ڶ���(g��)���}.���{(di��o)���߲��ظ��V�{(di��o)���ˆT�Լ��ش������һ��(g��)���}��ֻ��ش��ǡ����ǡ�����?y��n)�ֻ�б��{(di��o)���߱���֪���ش�����һ��(g��)���}�����Զ��猍(sh��)�����˻ش�.�Y(ji��)�����{(di��o)���800�ˣ��W(xu��)̖(h��o)��1��800������260�˻ش��ˡ��ǡ�.�ɴ˿��Թ�Ӌ(j��)�@800���н�(j��ng)�����֙C(j��)�όW(xu��)���˔�(sh��)��_________��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]()
��1����(sh��)![]() ���{(di��o)�f���^(q��)�g��
���{(di��o)�f���^(q��)�g��
��2��������(sh��)![]() �ĈD������ƽ��
�ĈD������ƽ��![]() ��(g��)��λ���ٌ��D���ϸ��c(di��n)�ęM����(bi��o)���L(zh��ng)��ԭ����
��(g��)��λ���ٌ��D���ϸ��c(di��n)�ęM����(bi��o)���L(zh��ng)��ԭ����![]() �����v����(bi��o)��׃���õ�����(sh��)
�����v����(bi��o)��׃���õ�����(sh��)![]() �ĈD����
�ĈD����![]() �����ֵ��ȡ�����ֵ�r(sh��)��
�����ֵ��ȡ�����ֵ�r(sh��)��![]() �ļ���.
�ļ���.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���P(gu��n)��ij�O(sh��)���ʹ������![]() ����֧���ľS���M(f��i)��
����֧���ľS���M(f��i)��![]() ���fԪ���������µĽy(t��ng)Ӌ(j��)�Y�ϣ�
���fԪ���������µĽy(t��ng)Ӌ(j��)�Y�ϣ�
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(1)�����Y�Ͽ�֪![]() ��(du��)
��(du��)![]() �ʾ������P(gu��n)�P(gu��n)ϵ.ԇ���λؚw���̣���
�ʾ������P(gu��n)�P(gu��n)ϵ.ԇ���λؚw���̣���![]() ��
�� ��
��
(2)��Ӌ(j��)ʹ�����ޞ�10��r(sh��)���S���M(f��i)���Ƕ��٣�
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com