
【題目】![]() 指數是用體重公斤數除以身高米數的平方得出的數字,是國際上常用的衡量人體胖瘦程度以及是否健康的一個標準.對于高中男體育特長生而言,當
指數是用體重公斤數除以身高米數的平方得出的數字,是國際上常用的衡量人體胖瘦程度以及是否健康的一個標準.對于高中男體育特長生而言,當![]() 數值大于或等于20.5時,我們說體重較重,當
數值大于或等于20.5時,我們說體重較重,當![]() 數值小于20.5時,我們說體重較輕,身高大于或等于
數值小于20.5時,我們說體重較輕,身高大于或等于![]() 我們說身高較高,身高小于170cm我們說身高較矮.
我們說身高較高,身高小于170cm我們說身高較矮.
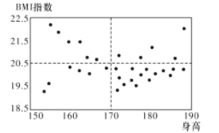
(Ⅰ)已知某高中共有32名男體育特長生,其身高與![]() 指數的數據如散點圖,請根據所得信息,完成下述列聯表,并判斷是否有
指數的數據如散點圖,請根據所得信息,完成下述列聯表,并判斷是否有![]() 的把握認為男生的身高對
的把握認為男生的身高對![]() 指數有影響.
指數有影響.
身高較矮 | 身高較高 | 合計 | |
體重較輕 | |||
體重較重 | |||
合計 |
(Ⅱ)①從上述32名男體育特長生中隨機選取8名,其身高和體重的數據如表所示:
編號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
身高 | 166 | 167 | 160 | 173 | 178 | 169 | 158 | 173 |
體重 | 57 | 58 | 53 | 61 | 66 | 57 | 50 | 66 |
根據最小二乘法的思想與公式求得線性回歸方程為![]() .利用已經求得的線性回歸方程,請完善下列殘差表,并求
.利用已經求得的線性回歸方程,請完善下列殘差表,并求![]() (解釋變量(身高)對于預報變量(體重)變化的貢獻值)(保留兩位有效數字);
(解釋變量(身高)對于預報變量(體重)變化的貢獻值)(保留兩位有效數字);
編號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
體重(kg) | 58 | 53 | 61 | 66 | 57 | 50 | 66 | |
殘差 |
|
|
|
|
|
|
|
②通過殘差分析,對于殘差的最大(絕對值)的那組數據,需要確認在樣本點的采集中是否有人為的錯誤,已知通過重新采集發現,該組數據的體重應該為![]() .小明重新根據最小二乘法的思想與公式,已算出
.小明重新根據最小二乘法的思想與公式,已算出![]() ,請在小明所算的基礎上求出男體育特長生的身高與體重的線性回歸方程.
,請在小明所算的基礎上求出男體育特長生的身高與體重的線性回歸方程.
參考數據:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
參考公式: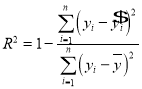 ,
,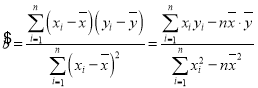 ,
,![]() ,
,![]() ,
,![]() .
.
| 0.10 | 0.05 | 0.01 | 0.005 |
| 2.706 | 3.811 | 6.635 | 7.879 |
【答案】(Ⅰ)列聯表詳見解析,沒有![]() 的把握認為男生的身高對
的把握認為男生的身高對![]() 指數有影響;(Ⅱ)①殘差表詳見解析,
指數有影響;(Ⅱ)①殘差表詳見解析,![]() 約為0.91;②
約為0.91;②![]() .
.
【解析】
(Ⅰ)根據散點圖完善列聯表,求出![]() 與表中對應臨界值比較即可判斷;(Ⅱ)①求出編號為8的數據的殘差,相應值代入公式
與表中對應臨界值比較即可判斷;(Ⅱ)①求出編號為8的數據的殘差,相應值代入公式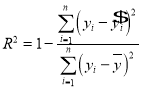 計算即可;②求出
計算即可;②求出![]() ,代入
,代入![]() 中即可求得
中即可求得![]() ,從而求得回歸方程.
,從而求得回歸方程.
(Ⅰ)
身高較矮 | 身高較高 | 合計 | |
體重較輕 | 6 | 15 | 21 |
體重較重 | 6 | 5 | 11 |
合計 | 12 | 20 | 32 |
由于![]() ,
,
因此沒有![]() 的把握認為男生的身高對
的把握認為男生的身高對![]() 指數有影響.
指數有影響.
(Ⅱ)①對編號為8的數據![]() ,完成殘差表如下所示:
,完成殘差表如下所示:
編號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
體重 | 57 | 58 | 53 | 61 | 66 | 57 | 50 | 66 |
殘差 | 0.1 | 0.3 | 0.9 |
|
|
|
| 3.5 |
![]()
 .
.
所以解釋變量(身高)對于預報變量(體重)變化的貢獻值![]() 約為0.91.
約為0.91.
②由①可知,第八組數據的體重應為58.此時,易知,![]() ,
,![]() ,
,
![]() ,
,
所以重新采集數據后,男體育特長生的身高與體重的線性回歸方程為![]() .
.


科目:高中數學 來源: 題型:
【題目】函數![]() 是定義域為
是定義域為![]() 的奇函數,且它的最小正周期是T,已知
的奇函數,且它的最小正周期是T,已知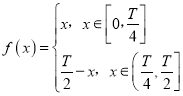 ,
,![]() .給出下列四個判斷:①對于給定的正整數
.給出下列四個判斷:①對于給定的正整數![]() ,存在
,存在![]() ,使得
,使得![]() 成立;②當a
成立;②當a![]() 時,對于給定的正整數
時,對于給定的正整數![]() ,存在
,存在![]() ,使得
,使得![]() 成立;③當
成立;③當![]()
![]() 時,函數
時,函數![]() 既有對稱軸又有對稱中心;④當
既有對稱軸又有對稱中心;④當![]()
![]() 時,
時,![]() 的值只有0或
的值只有0或![]() .其中正確判斷的有( )
.其中正確判斷的有( )
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,用四種不同顏色給圖中的A,B,C,D,E,F六個點涂色,要求每個點涂一種顏色,且圖中每條線段的兩個端點涂不同顏色,則不同的涂色方法用
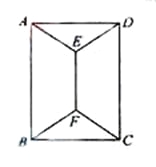
A.288種B.264種C.240種D.168種
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系中![]() 中,曲線C的參數方程
中,曲線C的參數方程![]() (
(![]() 為參數,
為參數,![]() ).以坐標原點為極點,x軸正半軸為極軸建立極坐標系,已知直線
).以坐標原點為極點,x軸正半軸為極軸建立極坐標系,已知直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)設P是曲線C上的一個動點,當![]() 時,求點P到直線
時,求點P到直線![]() 的距離的最大值;
的距離的最大值;
(2)若曲線C上所有的點均在直線![]() 的右下方,求t的取值范圍.
的右下方,求t的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】關于函數![]() ,有下述四個結論:
,有下述四個結論:
①![]() 是周期為
是周期為![]() 的函數;
的函數;
②![]() 在
在![]() 單調遞增;
單調遞增;
③![]() 在
在![]() 上有三個零點;
上有三個零點;
④![]() 的值域是
的值域是![]() .
.
其中所有正確結論的編號是( )
A.②③B.①③C.①③④D.①②④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】著名物理學家李政道說:“科學和藝術是不可分割的”.音樂中使用的樂音在高度上不是任意定的,它們是按照嚴格的數學方法確定的.我國明代的數學家、音樂理論家朱載填創立了十二平均律是第一個利用數學使音律公式化的人.十二平均律的生律法是精確規定八度的比例,把八度分成13個半音,使相鄰兩個半音之間的頻率比是常數,如下表所示,其中![]() 表示這些半音的頻率,它們滿足
表示這些半音的頻率,它們滿足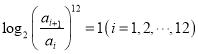 .若某一半音與
.若某一半音與![]() 的頻率之比為
的頻率之比為![]() ,則該半音為( )
,則該半音為( )
頻率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
半音 | C |
| D |
| E | F |
| G |
| A |
| B | C(八度) |
A.![]() B.GC.
B.GC.![]() D.A
D.A
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com