
【題目】設函數![]() 、
、![]() 滿足關系
滿足關系![]() ,其中
,其中![]() 是常數.
是常數.
(1)設![]() ,
,![]() ,求
,求![]() 的解析式;
的解析式;
(2)是否存在函數![]() 及常數
及常數![]() (
(![]() )使得
)使得![]() 恒成立?若存在,請你設計出函數
恒成立?若存在,請你設計出函數![]() 及常數
及常數![]() ;不存在,請說明理由;
;不存在,請說明理由;
(3)已知![]() 時,總有
時,總有![]() 成立,設函數
成立,設函數![]() (
(![]() )且
)且![]() ,對任意
,對任意![]() ,試比較
,試比較![]() 與
與![]() 的大小.
的大小.
【答案】(1)![]() ;(2)當
;(2)當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ;(3)
;(3)![]() .
.
【解析】
(1)由f(x)的解析式求出f(x+α)的解析式,相乘后得到函數g(x)的解析式;
(2)由逆向思維可知f(x)f(x+α)=sinxcosx,由此可得函數f(x)及一個α;
(3)由給出的f(x)求出g(x),從而求出sin[g(x)]與g(sinx),借助于![]() 可得答案.
可得答案.
(1)∵f(x)=cosx+sinx,![]()
∴f(x+α)=cosx﹣sinx;
∴g(x)=f(x)f(x+α)=(cosx+sinx)(cosx﹣sinx)
=cos2x﹣sin2x=cos2x;
(2)∵g(x)![]() sin2x=2sinxcosx,
sin2x=2sinxcosx,
若f(x)=![]() sinx,則f(x+α)=
sinx,則f(x+α)=![]() sin(x+α)=
sin(x+α)=![]() cosx
cosx![]()
∴f(x)=![]() sinx,常數
sinx,常數![]() ;
;
也可以設f(x)=![]() cosx,則f(x+α)=
cosx,則f(x+α)=![]() cos(x+α)=
cos(x+α)=![]() sinx
sinx![]()
∴f(x)=![]() cosx,常數
cosx,常數![]() ;
;
∴當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ;
;
(3)由題意g(x)=kx,sin[g(x)]=sinkx,g(sinx)=ksinx
又0<k<1,所以![]() ,
,
則![]() ,所以sinkx>ksinx,
,所以sinkx>ksinx,
即sin[g(x)]>g(sinx).


科目:高中數學 來源: 題型:
【題目】國家質量監督檢驗檢疫局于2004年5月31日發布了新的《車輛駕駛人員血液、呼氣酒精含量閥值與檢驗》國家標準.新標準規定,車輛駕駛人員血液中的酒精含量大于或等于![]() 毫克/百毫升,小于
毫克/百毫升,小于![]() 毫克/百毫升為飲酒駕車,血液中的酒精含量大于或等于
毫克/百毫升為飲酒駕車,血液中的酒精含量大于或等于![]() 毫克/百毫升為醉酒駕車.經過反復試驗,喝一瓶啤酒后酒精在人體血液中的變化規律的“散點圖”如下圖,該函數近似模型如下:
毫克/百毫升為醉酒駕車.經過反復試驗,喝一瓶啤酒后酒精在人體血液中的變化規律的“散點圖”如下圖,該函數近似模型如下: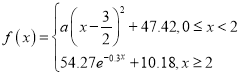 .
.
又已知剛好過1小時時測得酒精含量值為![]() 毫克/百毫升.根據上述條件,解答以下問題:
毫克/百毫升.根據上述條件,解答以下問題:
(1)試計算喝1瓶啤酒多少小時血液中的酒精含量達到最大值?最大值是多少?
(2)試計算喝1瓶啤酒后多少小時后才可以駕車?(時間以整分鐘計算)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是函數![]() 一個周期內的圖象,將
一個周期內的圖象,將![]() 圖象上所有點的橫坐標伸長為原來的2倍,縱坐標不變,再把所得圖象向右平移
圖象上所有點的橫坐標伸長為原來的2倍,縱坐標不變,再把所得圖象向右平移![]() 個單位長度,得到函數
個單位長度,得到函數![]() 的圖象.
的圖象.
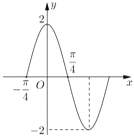
(1)求函數![]() 和
和![]() 的解析式;
的解析式;
(2)若![]() ,求
,求![]() 的所有可能的值;
的所有可能的值;
(3)求函數![]() (
(![]() 為正常數)在區間
為正常數)在區間![]() 內的所有零點之和.
內的所有零點之和.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業為提高生產質量,引入了一批新的生產設備,為了解生產情況,隨機抽取了新、舊設備生產的共200件產品進行質量檢測,統計得到產品的質量指標值如下表及圖(所有產品質量指標值均位于區間![]() 內),若質量指標值大于30,則說明該產品質量高,否則說明該產品質量一般.
內),若質量指標值大于30,則說明該產品質量高,否則說明該產品質量一般.
質量指標 | 頻數 |
| 2 |
| 8 |
| 10 |
| 30 |
| 20 |
| 10 |
合計 | 80 |
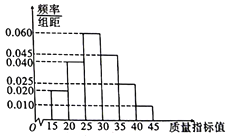
(1)根據上述圖表完成下列![]() 列聯表,并判斷是否有
列聯表,并判斷是否有![]() 的把握認為產品質量高與引人新設備有關;
的把握認為產品質量高與引人新設備有關;
新舊設備產品質量![]() 列聯表
列聯表
產品質量高 | 產品質量一般 | 合計 | |
新設備產品 | |||
舊設備產品 | |||
合計 |
(2)從舊設備生產的質量指標值位于區間![]() 的產品中,按分層抽樣抽取6件產品,再從這6件產品中隨機選取2件產品進行質量檢測,求至少有一件產品質量指標值位于
的產品中,按分層抽樣抽取6件產品,再從這6件產品中隨機選取2件產品進行質量檢測,求至少有一件產品質量指標值位于![]() 的概率.
的概率.
附: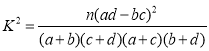 ,
,![]() .
.
| 0.10 | 0.05 | 0.01 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在平面直角坐標系![]() 上放置一個邊長為1的正方形
上放置一個邊長為1的正方形![]() ,此正方形
,此正方形![]() 沿
沿![]() 軸滾動(向左或向右均可),滾動開始時,點
軸滾動(向左或向右均可),滾動開始時,點![]() 位于原點處,設頂點
位于原點處,設頂點![]() 的縱坐標與橫坐標的函數關系式
的縱坐標與橫坐標的函數關系式![]() ,
,![]() ,該函數相鄰兩個零點之間的距離為
,該函數相鄰兩個零點之間的距離為![]() .
.
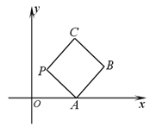
(1)寫出![]() 的值并求出頂點
的值并求出頂點![]() 到
到![]() 的最小運動路徑的長度
的最小運動路徑的長度![]() 的值;
的值;
(2)寫出函數![]() ,
,![]() ,
,![]() 的表達式;并研究該函數除周期外的基本性質(無需證明).
的表達式;并研究該函數除周期外的基本性質(無需證明).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】張軍自主創業,在網上經營一家干果店,銷售的干果中有松子、開心果、腰果、核桃,價格依次為120元/千克、80元/千克、70元/千克、40元千克,為增加銷量,張軍對這四種干果進行促銷:一次購買干果的總價達到150元,顧客就少付x(2x∈Z)元.每筆訂單顧客網上支付成功后,張軍會得到支付款的80%.
①若顧客一次購買松子和腰果各1千克,需要支付180元,則x=________;
②在促銷活動中,為保證張軍每筆訂單得到的金額均不低于促銷前總價的七折,則x的最大值為_____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,離心率為
,離心率為![]() ,直線
,直線![]() 與橢圓C交于A,B兩點,且
與橢圓C交于A,B兩點,且![]() .
.
(1)求橢圓C的方程.
(2)不經過點![]() 的直線
的直線![]() 被圓
被圓![]() 截得的弦長與橢圓C的長軸長相等,且直線
截得的弦長與橢圓C的長軸長相等,且直線![]() 與橢圓C交于D,E兩點,試判斷
與橢圓C交于D,E兩點,試判斷![]() 的周長是否為定值?若是,求出定值;若不是,請說明理由.
的周長是否為定值?若是,求出定值;若不是,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com