
【題目】為了檢測生產(chǎn)線上某種零件的質量,從產(chǎn)品中隨機抽取100個零件,測量其尺寸,得到如圖所示的頻率分布直方圖.若零件尺寸落在區(qū)間![]() 之內,則認為該零件合格,否則認為不合格.其中
之內,則認為該零件合格,否則認為不合格.其中![]() ,
,![]() 分別表示樣本的平均值和標準差,計算得
分別表示樣本的平均值和標準差,計算得![]() (同一組中的數(shù)據(jù)用該組區(qū)間的中點值作代表).
(同一組中的數(shù)據(jù)用該組區(qū)間的中點值作代表).
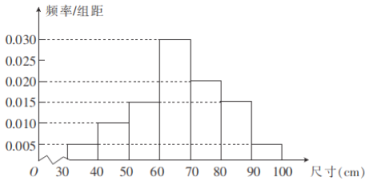
(1)已知一個零件的尺寸是![]() ,試判斷該零件是否合格;
,試判斷該零件是否合格;
(2)利用分層抽樣的方法從尺寸在![]() 的樣本中抽取6個零件,再從這6個零件中隨機抽取2個,求這2個零件中恰有1個尺寸小于
的樣本中抽取6個零件,再從這6個零件中隨機抽取2個,求這2個零件中恰有1個尺寸小于![]() 的概率.
的概率.
【答案】(1)該零件不合格.(2)![]()
【解析】
(1)根據(jù)頻率分布直方圖,計算出![]() 的區(qū)間,再判斷
的區(qū)間,再判斷![]() 是否屬于區(qū)間內,即可得答案;
是否屬于區(qū)間內,即可得答案;
(2)記這6個零件編號為:![]() ,再列出從這6個零件中隨機抽取2個的基本事件,記事件
,再列出從這6個零件中隨機抽取2個的基本事件,記事件![]() 為:“選出的2個零件中恰有1個尺寸小于
為:“選出的2個零件中恰有1個尺寸小于![]() ”,計算事件
”,計算事件![]() 包含的基本事件,利用古典概型計算概率,即可得答案;
包含的基本事件,利用古典概型計算概率,即可得答案;
(1)記各組的頻率為![]() ,依題意得
,依題意得
![]() ,
,
![]()
∴![]()
![]()
∴![]()
而![]() ,故該零件不合格.
,故該零件不合格.
(2)記前三組抽取的零件個數(shù)分別為![]()
∴![]() ,∴
,∴![]()
∴抽取出的6個零件中尺寸小于![]() 的有3個.
的有3個.
記這6個零件編號為:![]() (其中
(其中![]() 為尺寸小于
為尺寸小于![]() 的)
的)
記事件![]() 為:“選出的2個零件中恰有1個尺寸小于
為:“選出的2個零件中恰有1個尺寸小于![]() ”
”
∴從這6個零件中隨機抽取2個的基本事件有:
![]()
![]() 共15個.
共15個.
則事件![]() 包含的基本事件有:
包含的基本事件有:
![]() 共9個
共9個
∴![]()
∴這2個零件中恰有1個尺寸小于![]() 的概率為
的概率為![]() .
.


 能力評價系列答案
能力評價系列答案 唐印文化課時測評系列答案
唐印文化課時測評系列答案 導學與測試系列答案
導學與測試系列答案科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)討論函數(shù)![]() 的單調性;
的單調性;
(2)當![]() 時,判斷并說明函數(shù)
時,判斷并說明函數(shù)![]() 的零點個數(shù).若函數(shù)
的零點個數(shù).若函數(shù)![]() 所有零點均在區(qū)間
所有零點均在區(qū)間![]()
![]() 內,求
內,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】若函數(shù)![]() 滿足“存在正數(shù)
滿足“存在正數(shù)![]() ,使得對定義域內的每一個值
,使得對定義域內的每一個值![]() ,在其定義域內都存在
,在其定義域內都存在![]() ,使
,使![]() 成立”,則稱該函數(shù)為“依附函數(shù)”.
成立”,則稱該函數(shù)為“依附函數(shù)”.
(1)分別判斷函數(shù)①![]() ,②
,②![]() 是否為“依附函數(shù)”,并說明理由;
是否為“依附函數(shù)”,并說明理由;
(2)若函數(shù)![]() 的值域為
的值域為![]() ,求證:“
,求證:“![]() 是‘依附函數(shù)’”的充要條件是“
是‘依附函數(shù)’”的充要條件是“![]() ”.
”.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,直四棱柱![]() 中,四邊形
中,四邊形![]() 為梯形,
為梯形, ![]() ,且
,且![]() .過
.過![]() 三點的平面記為
三點的平面記為![]() ,
, ![]() 與
與![]() 的交點為
的交點為![]() .
.
(I)證明: ![]() 為
為![]() 的中點;
的中點;
(II)求此四棱柱被平面![]() 所分成上下兩部分的體積之比.
所分成上下兩部分的體積之比.

查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知數(shù)列{an}是單調遞增的等差數(shù)列,a2+a4=14且a2﹣1,a3+1,a4+7成等比數(shù)列.
(1)求數(shù)列{an}的通項公式;
(2)設數(shù)列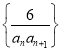 的前n項和為Sn.
的前n項和為Sn.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】當急需住院人數(shù)超過醫(yī)院所能收治的病人數(shù)量時就會發(fā)生“醫(yī)療資源擠兌”現(xiàn)象,在新冠肺炎爆發(fā)期間,境外某市每日下班后統(tǒng)計住院人數(shù),從中發(fā)現(xiàn):該市每日因新冠肺炎住院人數(shù)均比前一天下班后統(tǒng)計的住院人數(shù)增加約25%,但每日大約有200名新冠肺炎患者治愈出院,已知該市某天下班后有1000名新冠肺炎患者住院治療,該市的醫(yī)院共可收治4000名新冠肺炎患者,若繼續(xù)按照這樣的規(guī)律發(fā)展,該市因新冠肺炎疫情發(fā)生“醫(yī)療資源擠兌”現(xiàn)象,只需要約( )
參考數(shù)據(jù):![]() .
.
A.7天B.10天C.13天D.16天
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com