
【題目】已知函數![]() ,其中
,其中![]() .
.
(1)當![]() 時,求函數
時,求函數![]() 在
在![]() 處的切線方程;
處的切線方程;
(2)若函數![]() 存在兩個極值點
存在兩個極值點![]() ,求
,求![]() 的取值范圍;
的取值范圍;
(3)若不等式![]() 對任意的實數
對任意的實數![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1) ![]() .
.
(2) ![]() .
.
(3) ![]() .
.
【解析】分析:(1)求出![]() ,由
,由![]() 的值可得切點坐標,求出
的值可得切點坐標,求出![]() 的值,可得切線斜率,利用點斜式可得曲線
的值,可得切線斜率,利用點斜式可得曲線![]() 在點
在點![]() 處的切線方程;(2)
處的切線方程;(2)![]() 是方程
是方程![]() 的兩個正根,可得
的兩個正根,可得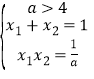 ,則
,則![]() 可化為
可化為![]() ,令
,令![]() ,可得
,可得![]() 在
在![]() 上單調遞增,所以
上單調遞增,所以![]() ;(3)
;(3)![]() 對任意的實數
對任意的實數![]() 恒成立,即
恒成立,即![]() 對任意的實數
對任意的實數![]() 恒成立,令
恒成立,令![]() ,利用導數研究函數的單調性,討論
,利用導數研究函數的單調性,討論![]() 的范圍,令
的范圍,令![]() 的最小值不小于零,可得到實數
的最小值不小于零,可得到實數![]() 的取值范圍.
的取值范圍.
詳解:(1)當![]() 時,
時,![]() ,故
,故![]() ,
,
且![]() ,故
,故![]()
所以函數![]() 在
在![]() 處的切線方程為
處的切線方程為![]()
(2)由![]() ,
,![]() 可得
可得![]()
因為函數![]() 存在兩個極值點
存在兩個極值點![]() ,所以
,所以![]() 是方程
是方程![]() 的兩個正根,
的兩個正根,
即![]() 的兩個正根為
的兩個正根為![]()
所以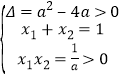 ,即
,即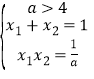
所以![]()
![]()
令![]() ,故
,故![]() ,
,![]() 在
在![]() 上單調遞增,
上單調遞增,
所以![]()
故![]() 得取值范圍是
得取值范圍是![]()
(3)據題意,![]() 對任意的實數
對任意的實數![]() 恒成立,
恒成立,
即![]() 對任意的實數
對任意的實數![]() 恒成立.
恒成立.
令![]() ,則
,則![]()
①若![]() ,當
,當![]() 時,
時,![]() ,故
,故![]() 符合題意;
符合題意;
②若![]() ,
,
(i)若![]() ,即
,即![]() ,則
,則![]() ,
,![]() 在
在![]() 上單調贈
上單調贈
所以當![]() 時,
時,![]() ,故
,故![]() 符合題意;
符合題意;
(ii)若![]() ,即
,即![]() ,令
,令![]() ,得
,得![]() (舍去),
(舍去),
![]() ,當
,當![]() 時,
時,![]() ,
,![]() 在
在![]() 上單調減;
上單調減;
當![]() 時,
時,![]() ,
,![]() 在
在![]() 上單調遞增,
上單調遞增,
所以存在![]() ,使得
,使得![]() ,與題意矛盾,
,與題意矛盾,
所以![]() 不符題意.
不符題意.
③若![]() ,令
,令![]() ,得
,得![]()
當![]() 時,
時,![]() ,
,![]() 在
在![]() 上單調增;當
上單調增;當![]() 時,
時,![]() ,
,
![]() 在
在![]() 上單調減.
上單調減.
首先證明:![]()
要證:![]() ,即要證:
,即要證:![]() ,只要證:
,只要證:![]()
因為![]() ,所以
,所以![]() ,故
,故![]()
所以![]()
其次證明,當![]() 時,
時,![]() 對任意的
對任意的![]() 都成立
都成立
令![]() ,則
,則![]() ,故
,故![]() 在
在![]() 上單調遞增,
上單調遞增,
所以![]() ,則
,則![]()
所以當![]() 時,
時,![]() 對任意的
對任意的![]() 都成立
都成立
所以當![]() 時,
時,![]()
即![]() ,與題意矛盾,故
,與題意矛盾,故![]() 不符題意,
不符題意,
綜上所述,實數![]() 的取值范圍是
的取值范圍是![]() .
.


科目:高中數學 來源: 題型:
【題目】如圖,AB是圓的直徑,PA垂直圓所在的平面,C是圓上的點.

(1)求證:平面PAC⊥平面PBC;
(2)若AB=2,AC=1,PA=1,求二面角C-PB-A的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某機械廠欲從![]() 米,
米,![]() 米的矩形鐵皮中裁剪出一個四邊形
米的矩形鐵皮中裁剪出一個四邊形![]() 加工成某儀器的零件,裁剪要求如下:點
加工成某儀器的零件,裁剪要求如下:點![]() 分別在邊
分別在邊![]() 上,且
上,且![]() ,
,![]() .設
.設![]() ,四邊形
,四邊形![]() 的面積為
的面積為![]() (單位:平方米).
(單位:平方米).

(1)求![]() 關于
關于![]() 的函數關系式,求出定義域;
的函數關系式,求出定義域;
(2)當![]() 的長為何值時,裁剪出的四邊形
的長為何值時,裁剪出的四邊形![]() 的面積最小,并求出最小值.
的面積最小,并求出最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某互聯網公司為了確定下一季度的前期廣告投入計劃,收集了近![]() 個月廣告投入量
個月廣告投入量![]() (單位:萬元)和收益
(單位:萬元)和收益![]() (單位:萬元)的數據如下表:
(單位:萬元)的數據如下表:
月份 |
|
|
|
|
|
|
廣告投入量 |
|
|
|
|
|
|
收益 |
|
|
|
|
|
|
他們分別用兩種模型①![]() ,②
,②![]() 分別進行擬合,得到相應的回歸方程并進行殘差分析,得到如圖所示的殘差圖及一些統計量的值:
分別進行擬合,得到相應的回歸方程并進行殘差分析,得到如圖所示的殘差圖及一些統計量的值:
|
|
|
|
|
|
|
|

(Ⅰ)根據殘差圖,比較模型①,②的擬合效果,應選擇哪個模型?并說明理由;
(Ⅱ)殘差絕對值大于![]() 的數據被認為是異常數據,需要剔除:
的數據被認為是異常數據,需要剔除:
(ⅰ)剔除異常數據后求出(Ⅰ)中所選模型的回歸方程
(ⅱ)若廣告投入量![]() 時,該模型收益的預報值是多少?
時,該模型收益的預報值是多少?
附:對于一組數據![]() ,
,![]() ,……,
,……,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為:
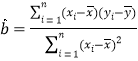
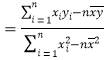 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,其中
,其中![]() .
.
![]() Ⅰ
Ⅰ![]() 當
當![]() 時,
時,![]() 恒成立,求a的取值范圍;
恒成立,求a的取值范圍;
![]() Ⅱ
Ⅱ![]() 設
設![]() 是定義在
是定義在![]() 上的函數,在
上的函數,在![]() 內任取
內任取![]() 個數
個數![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,設
,設![]() ,令
,令![]() ,
,![]() ,如果存在一個常數
,如果存在一個常數![]() ,使得
,使得![]() 恒成立,則稱函數
恒成立,則稱函數![]() 在區間
在區間![]() 上的具有性質P.試判斷函數
上的具有性質P.試判斷函數![]() 在區間
在區間![]() 上是否具有性質P?若具有性質P,請求出M的最小值;若不具有性質P,請說明理由.
上是否具有性質P?若具有性質P,請求出M的最小值;若不具有性質P,請說明理由.![]() 注:
注:![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓C:x2+y2﹣4x﹣6y+12=0,點A(3,5).
(1)將圓C的方程化為標準方程,并寫出圓C的圓心坐標及半徑r;
(2)求過點A的圓的切線方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com