
【題目】已知函數(shù)f(x)=ln x+ax2-2x,(a∈R,a≠0)
(1)若函數(shù)f(x)的圖象在x=1處的切線與x軸平行,求f(x)的單調(diào)區(qū)間;
(2)若f(x)≤ax在x∈[![]() ,+∞)上恒成立,求a的取值范圍.
,+∞)上恒成立,求a的取值范圍.
【答案】(1)單調(diào)遞增區(qū)間為(0,+∞),無(wú)單調(diào)遞減區(qū)間.(2)-4-4ln 2≤a<0.
【解析】
(1) f '(x)=![]() +2ax-2由f '(1)=1+2a-2=0,解得a=
+2ax-2由f '(1)=1+2a-2=0,解得a=![]() ,得f '(x)=
,得f '(x)=![]() ≥0恒成立,則單調(diào)區(qū)間可求;(2) f(x)≤ax轉(zhuǎn)化為ln x+ax2-2x-ax≤0,構(gòu)造函數(shù)g(x)=ln x+ax2-2x-ax,x∈[
≥0恒成立,則單調(diào)區(qū)間可求;(2) f(x)≤ax轉(zhuǎn)化為ln x+ax2-2x-ax≤0,構(gòu)造函數(shù)g(x)=ln x+ax2-2x-ax,x∈[![]() ,+∞),求導(dǎo)求其最大值即可求解
,+∞),求導(dǎo)求其最大值即可求解
(1)函數(shù)f(x)=ln x+ax2-2x,定義域?yàn)?/span>(0,+∞),f '(x)=![]() +2ax-2.
+2ax-2.
由已知f '(1)=1+2a-2=0,解得a=![]() ,
,
于是f '(x)=![]() ≥0恒成立,
≥0恒成立,
從而f(x)的單調(diào)遞增區(qū)間為(0,+∞),無(wú)單調(diào)遞減區(qū)間.
(2) f(x)≤ax轉(zhuǎn)化為ln x+ax2-2x-ax≤0,
設(shè)g(x)=ln x+ax2-2x-ax,x∈[![]() ,+∞),
,+∞),
則g'(x)=![]() +2ax-2-a=
+2ax-2-a=![]() .
.
①當(dāng)a<0時(shí),g(x)在[![]() ,+∞)上單調(diào)遞減,
,+∞)上單調(diào)遞減,
因而g(![]() )=ln
)=ln![]() +
+![]() a-1-
a-1-![]() a≤0,故-4-4ln 2≤a<0;
a≤0,故-4-4ln 2≤a<0;
②當(dāng)0<a<2時(shí),![]() ,g(x)在[
,g(x)在[![]() ,
,![]() ]上單調(diào)遞減,在(
]上單調(diào)遞減,在(![]() ,+∞)上單調(diào)遞增,
,+∞)上單調(diào)遞增,
因而g(x)∈[g(![]() ),+∞),不符合題意;
),+∞),不符合題意;
③當(dāng)a≥2時(shí),![]() ,g(x)在[
,g(x)在[![]() ,+∞)上單調(diào)遞增,
,+∞)上單調(diào)遞增,
因而g(x)∈[g(![]() ),+∞),不符合題意.
),+∞),不符合題意.
綜上,-4-4ln 2≤a<0.


 提分百分百檢測(cè)卷單元期末測(cè)試卷系列答案
提分百分百檢測(cè)卷單元期末測(cè)試卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)f(x)=|ax-2|+lnx(其中a為常數(shù))
(1)若a=0,求函數(shù)g(x)=![]() 的極值;
的極值;
(2)求函數(shù)f(x)的單調(diào)區(qū)間;
(3)令F(x)=f(x)-![]() ,當(dāng)a≥2時(shí),判斷函數(shù)F(x)在(0,1]上零點(diǎn)的個(gè)數(shù),并說(shuō)明理由.
,當(dāng)a≥2時(shí),判斷函數(shù)F(x)在(0,1]上零點(diǎn)的個(gè)數(shù),并說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某名校從![]() 年到
年到![]() 年考入清華,北大的人數(shù)可以通過(guò)以下表格反映出來(lái)。(為了方便計(jì)算,將
年考入清華,北大的人數(shù)可以通過(guò)以下表格反映出來(lái)。(為了方便計(jì)算,將![]() 年編號(hào)為
年編號(hào)為![]() ,
,![]() 年編為
年編為![]() ,以此類推……)
,以此類推……)
年份 |
|
|
|
|
|
|
|
|
|
|
人數(shù) |
|
|
|
|
|
|
|
|
|
|
(1)將這![]() 年的數(shù)據(jù)分為人數(shù)不少于
年的數(shù)據(jù)分為人數(shù)不少于![]() 人和少于
人和少于![]() 人兩組,按分層抽樣抽取
人兩組,按分層抽樣抽取![]() 年,問(wèn)考入清華、北大的人數(shù)不少于20的應(yīng)抽多少年?在抽取的這
年,問(wèn)考入清華、北大的人數(shù)不少于20的應(yīng)抽多少年?在抽取的這![]() 年里,若隨機(jī)的抽取兩年恰有一年考入清華、北大的人數(shù)不少于
年里,若隨機(jī)的抽取兩年恰有一年考入清華、北大的人數(shù)不少于![]() 的概率是多少?;
的概率是多少?;
(2)根據(jù)最近![]() 年的數(shù)據(jù),利用最小二乘法求出與之間的線性回歸方程,并用以預(yù)測(cè)
年的數(shù)據(jù),利用最小二乘法求出與之間的線性回歸方程,并用以預(yù)測(cè)![]() 年該校考入清華、北大的人數(shù)。(結(jié)果要求四舍五入至個(gè)位)
年該校考入清華、北大的人數(shù)。(結(jié)果要求四舍五入至個(gè)位)
參考公式: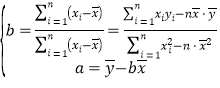
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某商場(chǎng)在一部向下運(yùn)行的手扶電梯終點(diǎn)的正上方豎直懸掛一幅廣告畫(huà).如圖,該電梯的高AB為4米,它所占水平地面的長(zhǎng)AC為8米.該廣告畫(huà)最高點(diǎn)E到地面的距離為10.5米,最低點(diǎn)D到地面的距離6.5米.假設(shè)某人的眼睛到腳底的距離MN為1.5米,他豎直站在此電梯上觀看DE的視角為θ.
(1)設(shè)此人到直線EC的距離為x米,試用x表示點(diǎn)M到地面的距離;
(2)此人到直線EC的距離為多少米時(shí),視角θ最大?

查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知橢圓![]() 的左、右焦點(diǎn)分別為
的左、右焦點(diǎn)分別為![]() ,點(diǎn)
,點(diǎn)![]() 也為拋物線
也為拋物線![]() 的焦點(diǎn).(1)若
的焦點(diǎn).(1)若![]() 為橢圓
為橢圓![]() 上兩點(diǎn),且線段
上兩點(diǎn),且線段![]() 的中點(diǎn)為
的中點(diǎn)為![]() ,求直線
,求直線![]() 的斜率;
的斜率;
(2)若過(guò)橢圓![]() 的右焦點(diǎn)
的右焦點(diǎn)![]() 作兩條互相垂直的直線分別交橢圓于
作兩條互相垂直的直線分別交橢圓于![]() 和
和![]() ,設(shè)線段
,設(shè)線段![]() 的長(zhǎng)分別為
的長(zhǎng)分別為![]() ,證明
,證明![]() 是定值.
是定值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,已知三棱錐O-ABC的三條側(cè)棱OA,OB,OC兩兩垂直, ![]() 為等邊三角形,
為等邊三角形, ![]() 為
為![]() 內(nèi)部一點(diǎn),點(diǎn)
內(nèi)部一點(diǎn),點(diǎn)![]() 在
在![]() 的延長(zhǎng)線上,且PA=PB.
的延長(zhǎng)線上,且PA=PB.
(Ⅰ)證明:OA=OB;
(Ⅱ)證明:平面PAB平面POC.

查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在標(biāo)有“甲”的袋中有![]() 個(gè)紅球和
個(gè)紅球和![]() 個(gè)白球,這些球除顏色外完全相同.
個(gè)白球,這些球除顏色外完全相同.
(Ⅰ)若從袋中依次取出![]() 個(gè)球,求在第一次取到紅球的條件下,后兩次均取到白球的概率;
個(gè)球,求在第一次取到紅球的條件下,后兩次均取到白球的概率;
(Ⅱ)現(xiàn)從甲袋中取出個(gè)![]() 紅球,
紅球, ![]() 個(gè)白球,裝入標(biāo)有“乙”的空袋.若從甲袋中任取
個(gè)白球,裝入標(biāo)有“乙”的空袋.若從甲袋中任取![]() 球,乙袋中任取
球,乙袋中任取![]() 球,記取出的紅球的個(gè)數(shù)為
球,記取出的紅球的個(gè)數(shù)為![]() ,求
,求![]() 的分布列和數(shù)學(xué)期望
的分布列和數(shù)學(xué)期望![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知![]() 是奇函數(shù).
是奇函數(shù).
(1)求實(shí)數(shù)![]() 的值;
的值;
(2)求函數(shù)![]() 在
在![]() 上的值域;
上的值域;
(3)令![]() ,求不等式
,求不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知橢圓![]() ,三點(diǎn)
,三點(diǎn) 中恰有二點(diǎn)在橢圓
中恰有二點(diǎn)在橢圓![]() 上,且離心率為
上,且離心率為![]() 。
。

(1)求橢圓![]() 的方程;
的方程;
(2)設(shè)![]() 為橢圓
為橢圓![]() 上任一點(diǎn),
上任一點(diǎn), ![]() 為橢圓
為橢圓![]() 的左右頂點(diǎn),
的左右頂點(diǎn), ![]() 為
為![]() 中點(diǎn),求證:直線
中點(diǎn),求證:直線![]() 與直線
與直線![]() 它們的斜率之積為定值;
它們的斜率之積為定值;
(3)若橢圓![]() 的右焦點(diǎn)為
的右焦點(diǎn)為![]() ,過(guò)
,過(guò)![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,求證:直線
,求證:直線![]() 與直線
與直線![]() 斜率之和為定值。
斜率之和為定值。
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com