Question

【題目】已知奇函數.

（1）求函數的值域；

（2）判斷函數的單調性，并給出證明；

（3）若函數在區間上有兩個不同的零點，求m的取值范圍.

Answer 1

【答案】（1）；（2）見解析；（3）.

【解析】

（1）根據當有意義的奇函數圖象過坐標原點，，求得參數的值，利用不等式的性質求函數的值域，得到結果；

（2）應用定義判斷并證明函數的單調性；

（3）利用函數零點的個數，對式子進行化簡，轉化為對應方程有兩個不等實根，考慮函數圖象的走向，求得結果.

（1）因為函數為奇函數，且定義域為R，

所以有，即，解得，

所以，

因為，所以，，

所以，，

所以函數的值域為；

（2）為上的增函數，證明如下：

任取，且，則

，

因為，所以，所以，

所以，

所以函數為上的增函數；

（3）函數在區間上有兩個不同的零點，

即在上有兩個不同的實數根，

整理得，

設，所以，

則當時，，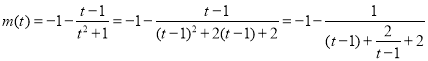

綜合考慮可得在上單調遞減，在上單調遞增，

且，，，

要使函數有兩個零點，可以得到的取值范圍是.