
【題目】已知函數![]() ,
,![]() .
.
(Ⅰ)求函數![]() 的單調區間;
的單調區間;
(Ⅱ)若對任意的![]() ,總存在
,總存在![]() ,使得
,使得![]() 成立,求實數
成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(Ⅰ)見解析;(Ⅱ)![]() .
.
【解析】
(Ⅰ)求導求出![]() ,對
,對![]() 分類討論,以
分類討論,以![]() (或
(或![]() )是否恒成立作為分類標準,當
)是否恒成立作為分類標準,當![]() (或
(或![]() )不恒成立,求出
)不恒成立,求出![]() 的解,即可得出結論;
的解,即可得出結論;
(Ⅱ)構造函數![]() ,原問題轉化為對任意的
,原問題轉化為對任意的![]() ,總存在
,總存在![]() ,使得
,使得![]() 成立,即
成立,即![]() ,利用求導方法,求出
,利用求導方法,求出![]() 的最值,將問題轉化為
的最值,將問題轉化為![]() 與
與![]() 的函數關系,即可求解.
的函數關系,即可求解.
(Ⅰ)![]() 的定義域為
的定義域為![]() ,
,![]() ,
,
令![]() ,
,![]() ,
,
(1)當![]() ,即
,即![]() 時,
時,
![]() 恒成立,即
恒成立,即![]() 恒成立,
恒成立,
故函數![]() 的單增區間為
的單增區間為![]() ,無單減區間.
,無單減區間.
(2)當![]() ,即
,即![]() 時,由
時,由![]() 解得
解得
![]() 或
或![]() ,
,
i)當![]() 時,
時,![]() ,
,
所以當![]() 或
或![]() 時
時![]() ,
,
當![]() 時
時![]() .
.
ii)當![]() 時,
時,![]() ,
,
所以當![]() 時
時![]() ,
,
當![]() 時
時![]() ;
;
綜上所述:
當![]() 時,函數
時,函數![]() 的單增區間為
的單增區間為![]() ,無單減區間.
,無單減區間.
當![]() 時,函數
時,函數![]() 的單增區間為
的單增區間為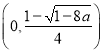 和
和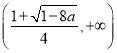 ,
,
單減區間為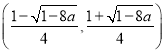 .
.
當![]() 時,函數
時,函數![]() 的單增區間為
的單增區間為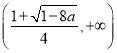 ,
,
單減區間為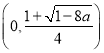 .
.
(Ⅱ)令![]() ,
,![]() .
.
原問題等價于:對任意的![]() ,總存在
,總存在![]() ,
,
使得![]() 成立,即
成立,即![]() .
.
∵![]() ,∵
,∵![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() 在
在![]() 上單調遞增,
上單調遞增,
∴![]() ,
,
即![]() 對任意的
對任意的![]() 恒成立,
恒成立,
令![]() ,
,![]() ,只需
,只需![]() ,
,
![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
∴![]() 在
在![]() 上單調遞增,∴
上單調遞增,∴![]() ,
,
所以![]() .
.


 寒假樂園北京教育出版社系列答案
寒假樂園北京教育出版社系列答案科目:高中數學 來源: 題型:
【題目】港珠澳大橋于2018年10月2刻日正式通車,它是中國境內一座連接香港、珠海和澳門的橋隧工程,橋隧全長55千米.橋面為雙向六車道高速公路,大橋通行限速100km/h,現對大橋某路段上1000輛汽車的行駛速度進行抽樣調查.畫出頻率分布直方圖(如圖),根據直方圖估計在此路段上汽車行駛速度在區間[85,90)的車輛數和行駛速度超過90km/h的頻率分別為( )
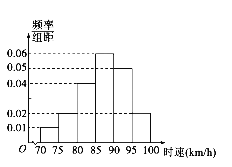
A. 300,![]() B. 300,
B. 300,![]() C. 60,
C. 60,![]() D. 60,
D. 60,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設P是拋物線y2=4x上的一個動點,F為拋物線的焦點,記點P到點A(-1,1)的距離與點P到直線x= - 1的距離之和的最小值為M,若B(3,2),記|PB|+|PF|的最小值為N,則M+N= ______________
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1為某省2018年1~4月快遞業務量統計圖,圖2是該省2018年1~4月快遞業務收入統計圖,下列對統計圖理解錯誤的是( )


A. 2018年1~4月的業務量,3月最高,2月最低,差值接近2000萬件
B. 2018年1~4月的業務量同比增長率均超過50%,在3月底最高
C. 從兩圖來看,2018年1~4月中的同一個月的快遞業務量與收入的同比增長率并不完全一致
D. 從1~4月來看,該省在2018年快遞業務收入同比增長率逐月增長
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某購物網站對在7座城市的線下體驗店的廣告費指出![]() 萬元和銷售額
萬元和銷售額![]() 萬元的數據統計如下表:
萬元的數據統計如下表:
城市 | A | B | C | D | E | F | G |
廣告費支出 | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
銷售額 | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
(1)若用線性回歸模型擬合y與x關系,求y關于x的線性回歸方程.
(2)若用對數函數回歸模型擬合y與x的關系,可得回歸方程![]() ,經計算對數函數回歸模型的相關指數約為0.95,請說明選擇哪個回歸模型更合適,并用此模型預測A城市的廣告費用支出8萬元時的銷售額.
,經計算對數函數回歸模型的相關指數約為0.95,請說明選擇哪個回歸模型更合適,并用此模型預測A城市的廣告費用支出8萬元時的銷售額.
參考數據:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
參考公式: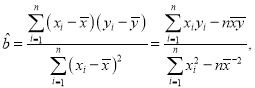
![]() ,
,
相關指數: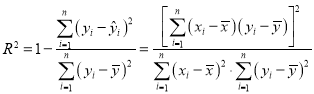 (注意:
(注意:![]() 與
與![]() 公式中的相似之處)
公式中的相似之處)
查看答案和解析>>
科目:高中數學 來源: 題型:
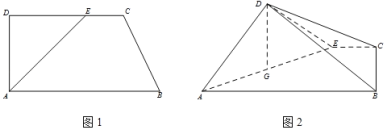
【題目】如圖,在直角梯形![]() 中,
中,![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]() ,點
,點![]() 在
在![]() 上,且
上,且![]() ,將
,將![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() (如圖),
(如圖),![]() 為
為![]() 中點.
中點.
(Ⅰ)求證:![]() 平面
平面![]() ;
;
(Ⅱ)求四棱錐![]() 的體積;
的體積;
(Ⅲ)在線段![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com