
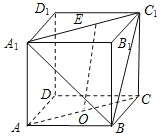
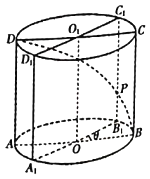
【題目】在正方體ABCD﹣A1B1C1D1中,O為線段AC的中點(diǎn),點(diǎn)E在線段A1C1上,則直線OE與平面A1BC1所成角的正弦值的取值范圍是( )
A.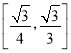 B.
B.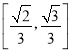 C.
C.![]() D.
D.![]()
【答案】B
【解析】
設(shè)正方體的邊長為![]() ,以
,以![]() 、
、![]() 、
、![]() 分別為
分別為![]() 軸,建立空間直角坐標(biāo)系,設(shè)
軸,建立空間直角坐標(biāo)系,設(shè)![]() ,
,![]() ,則
,則![]() ,再求出平面A1BC1 的一個法向量,直線OE與平面A1BC1所成角為
,再求出平面A1BC1 的一個法向量,直線OE與平面A1BC1所成角為![]() ,利用空間向量的數(shù)量積,由
,利用空間向量的數(shù)量積,由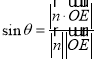 即可求解.
即可求解.
設(shè)正方體的邊長為![]() ,以
,以![]() 、
、![]() 、
、![]() 分別為
分別為![]() 軸,
軸,
建立空間直角坐標(biāo)系,如圖所示:
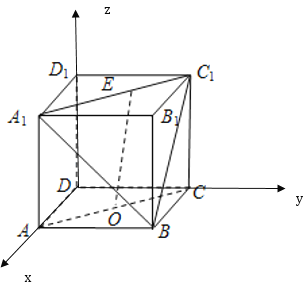
則![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
設(shè)![]() ,
,![]() ,則
,則![]() ,
,
設(shè)平面A1BC1 的一個法向量為![]() ,
,
則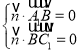 ,可得
,可得![]() ,
,
令![]() ,則
,則![]() ,所以
,所以![]() ,
,
設(shè)直線OE與平面A1BC1所成角為![]() ,
,
則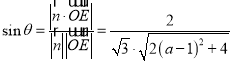 ,
,
當(dāng)![]() 時,
時,![]() 取最大值為
取最大值為![]() ,
,
當(dāng)![]() 或
或![]() 時,
時,![]() 取最小值為
取最小值為![]() ,
,
故直線OE與平面A1BC1所成角的正弦值的取值范圍是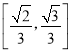 .
.
故選:B


 寶貝計劃期末沖刺奪100分系列答案
寶貝計劃期末沖刺奪100分系列答案 能考試全能100分系列答案
能考試全能100分系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】鯉魚是中國五千年文化傳承的載體之一,它既是拼搏進(jìn)取、敢于突破自我、敢于冒險奮進(jìn)精神的載體,又是富裕、吉慶、幸運(yùn)的美好象征.某水產(chǎn)養(yǎng)殖研究所為發(fā)揚(yáng)傳統(tǒng)文化,準(zhǔn)備進(jìn)行“中國紅鯉”和“中華彩鯉”雜交育種實(shí)驗.研究所對200尾中國紅鯉和160尾中華彩鯉幼苗進(jìn)行2個月培育后,將根據(jù)體長分別選擇生長快的10尾中國紅鯉和8尾中華彩鯉作為種魚進(jìn)一步培育.為了解培育2個月后全體幼魚的體長情況,按照品種進(jìn)行分層抽樣,其中共抽取40尾中國紅鯉的體長數(shù)據(jù)(單位:![]() )如下:
)如下:
5 | 6 | 7 | 7.5 | 8 | 8.4 | 4 | 3.5 | 4.5 | 4.3 |
5 | 4 | 3 | 2.5 | 4 | 1.6 | 6 | 6.5 | 5.5 | 5.7 |
3.1 | 5.2 | 4.4 | 5 | 6.4 | 3.5 | 7 | 4 | 3 | 3.4 |
6.9 | 4.8 | 5.6 | 5 | 5.6 | 6.5 | 3 | 6 | 7 | 6.6 |
(1)根據(jù)以上樣本數(shù)據(jù)推斷,若某尾中國紅鯉的體長為![]() ,它能否被選為種魚?說明理由;
,它能否被選為種魚?說明理由;
(2)通過計算得到中國紅鯉樣本數(shù)據(jù)平均值為![]() ,中華彩鯉樣本數(shù)據(jù)平均值為
,中華彩鯉樣本數(shù)據(jù)平均值為![]() ,求所有樣本數(shù)據(jù)的平均值;
,求所有樣本數(shù)據(jù)的平均值;
(3)如果將8尾中華彩鯉種魚隨機(jī)兩兩組合,求體長最長的2尾組合到一起的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線![]() 的焦點(diǎn)到其準(zhǔn)線的距離為
的焦點(diǎn)到其準(zhǔn)線的距離為![]() .
.
(1)求拋物線![]() 的方程;
的方程;
(2)設(shè)直線![]() 與拋物線
與拋物線![]() 相交于
相交于![]() 兩點(diǎn),問拋物線
兩點(diǎn),問拋物線![]() 上是否存在點(diǎn)
上是否存在點(diǎn)![]() ,使得
,使得![]() 是正三角形?若存在,求出點(diǎn)
是正三角形?若存在,求出點(diǎn)![]() 的坐標(biāo);若不存在,請說明理由.
的坐標(biāo);若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的右頂點(diǎn)為
的右頂點(diǎn)為![]() ,左焦點(diǎn)為
,左焦點(diǎn)為![]() ,離心率
,離心率![]() ,過點(diǎn)
,過點(diǎn)![]() 的直線與橢圓交于另一個點(diǎn)
的直線與橢圓交于另一個點(diǎn)![]() ,且點(diǎn)
,且點(diǎn)![]() 在
在![]() 軸上的射影恰好為點(diǎn)
軸上的射影恰好為點(diǎn)![]() ,若
,若![]() .
.
(1)求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)過圓![]() 上任意一點(diǎn)
上任意一點(diǎn)![]() 作圓
作圓![]() 的切線
的切線![]() 與橢圓交于
與橢圓交于![]() ,
,![]() 兩點(diǎn),以
兩點(diǎn),以![]() 為直徑的圓是否過定點(diǎn),如過定點(diǎn),求出該定點(diǎn);若不過定點(diǎn),請說明理由.
為直徑的圓是否過定點(diǎn),如過定點(diǎn),求出該定點(diǎn);若不過定點(diǎn),請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標(biāo)系![]() 中,直線
中,直線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)),曲線
為參數(shù)),曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)),以該直角坐標(biāo)系的原點(diǎn)
為參數(shù)),以該直角坐標(biāo)系的原點(diǎn)![]() 為極點(diǎn),
為極點(diǎn),![]() 軸的非負(fù)半軸為極軸建立極坐標(biāo)系,曲線
軸的非負(fù)半軸為極軸建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(Ⅰ)分別求曲線![]() 的極坐標(biāo)方程和曲線
的極坐標(biāo)方程和曲線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(Ⅱ)設(shè)直線![]() 交曲線
交曲線![]() 于
于![]() ,
,![]() 兩點(diǎn),交曲線
兩點(diǎn),交曲線![]() 于
于![]() ,
,![]() 兩點(diǎn),求
兩點(diǎn),求![]() 的長.
的長.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓C:![]() 1(a>b>0),其右焦點(diǎn)為F(1,0),離心率為
1(a>b>0),其右焦點(diǎn)為F(1,0),離心率為![]() .
.
(Ⅰ)求橢圓C的方程;
(Ⅱ)過點(diǎn)F作傾斜角為α的直線l,與橢圓C交于P,Q兩點(diǎn).
(ⅰ)當(dāng)![]() 時,求△OPQ(O為坐標(biāo)原點(diǎn))的面積;
時,求△OPQ(O為坐標(biāo)原點(diǎn))的面積;
(ⅱ)隨著α的變化,試猜想|PQ|的取值范圍,并證明你的猜想.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知圓柱![]() ,底面半徑為1,高為2,
,底面半徑為1,高為2,![]() 是圓柱的一個軸截面,動點(diǎn)
是圓柱的一個軸截面,動點(diǎn)![]() 從點(diǎn)
從點(diǎn)![]() 出發(fā)沿著圓柱的側(cè)面到達(dá)點(diǎn)
出發(fā)沿著圓柱的側(cè)面到達(dá)點(diǎn)![]() ,其路徑最短時在側(cè)面留下的曲線記為
,其路徑最短時在側(cè)面留下的曲線記為![]() :將軸截面
:將軸截面![]() 繞著軸
繞著軸![]() ,逆時針旋轉(zhuǎn)
,逆時針旋轉(zhuǎn)![]()
![]() 角到
角到![]() 位置,邊
位置,邊![]() 與曲線
與曲線![]() 相交于點(diǎn)
相交于點(diǎn)![]() .
.
(1)當(dāng)![]() 時,求證:直線
時,求證:直線![]() 平面
平面![]() ;
;
(2)當(dāng)![]() 時,求二面角
時,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的離心率為
的離心率為![]() ,左、右頂點(diǎn)分別為
,左、右頂點(diǎn)分別為![]() 、
、![]() ,過左焦點(diǎn)的直線
,過左焦點(diǎn)的直線![]() 交橢圓
交橢圓![]() 于
于![]() 、
、![]() 兩點(diǎn)(異于
兩點(diǎn)(異于![]() 、
、![]() 兩點(diǎn)),當(dāng)直線
兩點(diǎn)),當(dāng)直線![]() 垂直于
垂直于![]() 軸時,四邊形
軸時,四邊形![]() 的面積為6.
的面積為6.
(1)求橢圓的方程;
(2)設(shè)直線![]() 、
、![]() 的交點(diǎn)為
的交點(diǎn)為![]() ;試問
;試問![]() 的橫坐標(biāo)是否為定值?若是,求出定值;若不是,請說明理由.
的橫坐標(biāo)是否為定值?若是,求出定值;若不是,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】阿基米德(公元前![]() 年—公元前
年—公元前![]() 年)不僅是著名的物理學(xué)家,也是著名的數(shù)學(xué)家,他利用“逼近法”得到橢圓的面積除以圓周率
年)不僅是著名的物理學(xué)家,也是著名的數(shù)學(xué)家,他利用“逼近法”得到橢圓的面積除以圓周率![]() 等于橢圓的長半軸與短半軸的乘積.已知平面直角坐標(biāo)系
等于橢圓的長半軸與短半軸的乘積.已知平面直角坐標(biāo)系![]() 中,橢圓
中,橢圓![]() :
:![]()
![]() 的面積為
的面積為![]() ,兩焦點(diǎn)與短軸的一個頂點(diǎn)構(gòu)成等邊三角形.
,兩焦點(diǎn)與短軸的一個頂點(diǎn)構(gòu)成等邊三角形.
(1)求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)過點(diǎn)![]() 的直線
的直線![]() 與
與![]() 交于不同的兩點(diǎn)
交于不同的兩點(diǎn)![]() ,求
,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com