
【題目】已知函數f(x)=ln(2+ax)(a>0),![]() (b∈R).
(b∈R).
(1)若函數f(x)的圖象在點(3,f(3))處的切線與函數g(x)的圖象在點(1,g(1))處的切線平行,求a,b之間的關系;
(2)在(1)的條件下,若b=a,且f(x)≥mg(x)對任意x∈[![]() ,+∞)恒成立,求實數m的取值范圍.
,+∞)恒成立,求實數m的取值范圍.
【答案】(1)![]() (2)(-∞,
(2)(-∞,![]() ]
]
【解析】
(1)對函數求導,再根據在兩點處的切線的斜率相等,得到f'(3)=g'(1),進而得到參數的關系;(2)先由b=a求出參數值,令![]() ,則問題轉化為h(x)≥0對任意x∈[
,則問題轉化為h(x)≥0對任意x∈[![]() ,+∞)恒成立,對m分情況,對h(x)求導研究函數的單調性,得到函數最小值,最小值大于等于0即可.
,+∞)恒成立,對m分情況,對h(x)求導研究函數的單調性,得到函數最小值,最小值大于等于0即可.
(1)![]() ,
,![]() ,
,
因為函數f(x)的圖象在點(3,f(3))處的切線與函數g(x)的圖象在點(1,g(1))處的切線平行,
所以f'(3)=g'(1).
所以![]() ,化簡得
,化簡得![]() .
.
(2)由(1)得,![]() ,
,
若b=a,則![]() ,解得a=2或
,解得a=2或![]() (舍去,因為a>0).
(舍去,因為a>0).
所以a=b=2.
所以f(x)=ln(2+2x),![]() .
.
令2+2x>0,得x>-1,則函數f(x)=ln(2+2x)的定義域是(-1,+∞);
令1+x≠0,得x≠-1,則函數![]() 的定義域是(-∞,-1)∪(-1,+∞).
的定義域是(-∞,-1)∪(-1,+∞).
f(x)≥mg(x)對任意x∈[![]() ,+∞)恒成立,即
,+∞)恒成立,即![]() 對任意x∈[
對任意x∈[![]() ,+∞)恒成立.
,+∞)恒成立.
令![]() ,則問題轉化為h(x)≥0對任意x∈[
,則問題轉化為h(x)≥0對任意x∈[![]() ,+∞)恒成立.
,+∞)恒成立.
![]() .
.
①當![]() ,即x+1-m≥0時,h'(x)≥0且h'(x)不恒為0,
,即x+1-m≥0時,h'(x)≥0且h'(x)不恒為0,
所以函數![]() 在區間[
在區間[![]() ,+∞)上單調遞增.
,+∞)上單調遞增.
又![]() ,
,
所以h(x)≥0對任意x∈[![]() ,+∞)恒成立.故
,+∞)恒成立.故![]() 符合題意.
符合題意.
②當![]() 時,令
時,令![]() ,得
,得![]() ;
;
令![]() ,得x>m-1.
,得x>m-1.
所以函數![]() 在區間[
在區間[![]() ,m-1)上單調遞減,在區間(m-1,+∞)上單調遞增,
,m-1)上單調遞減,在區間(m-1,+∞)上單調遞增,
所以![]() .即當
.即當![]() 時,存在
時,存在![]() ,使h(x0)<0.
,使h(x0)<0.
故知h(x)≥0對任意x∈[![]() ,+∞)不恒成立.故
,+∞)不恒成立.故![]() 不符合題意.
不符合題意.
綜上可知,實數m的取值范圍是(-∞,![]() ].
].


 每日10分鐘口算心算速算天天練系列答案
每日10分鐘口算心算速算天天練系列答案科目:高中數學 來源: 題型:
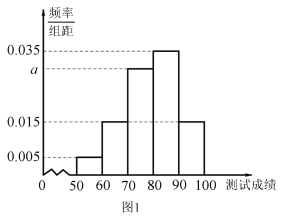
【題目】順義區教委對本區高一,高二年級學生體質健康測試成績進行抽樣分析.學生測試成績滿分為100分,90分及以上為優秀,60分以下為不及格.先從兩個年級各抽取100名學生的測試成績.其中高一年級學生測試成績統計結果如圖1,高二年級學生測試成績統計結果如表1.
分組 | 人數 |
|
|
|
|
|
|
|
|
|
|
表1
(1)求圖1中a的值;
(2)為了調查測試成績不及格的同學的具體情況,決定從樣本中不及格的學生中抽取3人,用X表示抽取的3人中高二年級的學生人數.求X的分布列及均值;
(3)若用以上抽樣數據估計全區學生體質健康情況.用Y表示從全區高二年級全部學生中任取3人中成績優秀的人數,求EY的值;
(4)用![]() ,
,![]() ,分別表示樣本中高一,高二年級學生測試成績的方差,比較其大小(只需寫出結果).
,分別表示樣本中高一,高二年級學生測試成績的方差,比較其大小(只需寫出結果).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】王明、李東、張紅三位同學在第一、第二學期消費的部分文具的數量如表所示:
姓名 | 第一學期 | 第二學期 | ||||||
筆記本 | 練習本 | 水筆 | 鉛筆 | 筆記本 | 練習本 | 水筆 | 鉛筆 | |
王明 | 3 | 5 | 2 | 4 | 4 | 6 | 3 | 3 |
李東 | 2 | 6 | 3 | 3 | 4 | 8 | 5 | 2 |
張紅 | 4 | 7 | 4 | 2 | 5 | 10 | 6 | 4 |
若筆記本的單價為每本5元;練習本每本2元;水筆每支3元;鉛筆每支1元.求三位學生在這些文具上各自花費的金額.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,有一種游戲畫板,要求參與者用六種顏色給畫板涂色,這六種顏色分別為紅色、黃色1、黃色2、黃色3、金色1、金色2,其中黃色1、黃色2、黃色3是三種不同的顏色,金色1、金色2是兩種不同的顏色,要求紅色不在兩端,黃色1、黃色2、黃色3有且僅有兩種相鄰,則不同的涂色方案有( )

A.120種B.240種C.144種D.288種
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓A:(x+1)2+y2=16,圓C過點B(1,0)且與圓A相切,設圓心C的軌跡為曲線E.
(Ⅰ)求曲線E的方程;
(Ⅱ)過點B作兩條互相垂直的直線l1,l2,直線l1與E交于M,N兩點,直線l2與圓A交于P,Q兩點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學為了解中學生的課外閱讀時間,決定在該中學的1200名男生和800名女生中按分層抽樣的方法抽取20名學生,對他們的課外閱讀時間進行問卷調查。現在按課外閱讀時間的情況將學生分成三類:A類(不參加課外閱讀),B類(參加課外閱讀,但平均每周參加課外閱讀的時間不超過3小時),C類(參加課外閱讀,且平均每周參加課外閱讀的時間超過3小時)。調查結果如下表:
A類 | B類 | C類 | |
男生 | x | 5 | 3 |
女生 | y | 3 | 3 |
(I)求出表中x,y的值;
(II)根據表中的統計數據,完成下面的列聯表,并判斷是否有90%的把握認為“參加課外閱讀與否”與性別有關;
男生 | 女生 | 總計 | |
不參加課外閱讀 | |||
參加課外閱讀 | |||
總計 |
(III)從抽出的女生中再隨機抽取3人進一步了解情況,記X為抽取的這3名女生中A類人數和C類人數差的絕對值,求X的數學期望。
附:K2=![]() )
)
P(K2≥k0) | 0.10 | 0.01 | |
k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市為了了解民眾對開展創建文明城市工作以來的滿意度,隨機調查了40名群眾,并將他們隨機分成A,B兩組,每組20人,A組群眾給第一階段的創文工作評分,B組群眾給第二階段的創文工作評分,根據兩組群眾的評分繪制了如下莖葉圖:
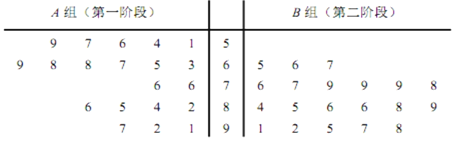
![]() 根據莖葉圖比較群眾對兩個階段創文工作滿意度評分的平均值及集中程度
根據莖葉圖比較群眾對兩個階段創文工作滿意度評分的平均值及集中程度![]() 不要求計算出具體值,給出結論即可
不要求計算出具體值,給出結論即可![]() ;
;
![]() 根據群眾的評分將滿意度從低到高分為三個等級:
根據群眾的評分將滿意度從低到高分為三個等級:
滿意度評分 | 低于70分 | 70分到89分 | 不低于90分 |
滿意度等級 | 不滿意 | 滿意 | 非常滿意 |
![]() 假設兩組群眾的評價結果相互獨立,由頻率估計概率,求創文工作第二階段的民眾滿意度等級高于第一階段的概率;
假設兩組群眾的評價結果相互獨立,由頻率估計概率,求創文工作第二階段的民眾滿意度等級高于第一階段的概率;
![]() 從這40名群眾中隨機抽取2人,記X表示滿意度等級為“非常滿意”的群眾人數,求X的分布列與數學期望.
從這40名群眾中隨機抽取2人,記X表示滿意度等級為“非常滿意”的群眾人數,求X的分布列與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
極坐標系的極點為直角坐標系![]() 的原點,極軸為
的原點,極軸為![]() 軸的正半軸,兩種坐標系中的長度單位相同,已知曲線
軸的正半軸,兩種坐標系中的長度單位相同,已知曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求![]() 的直角坐標方程;
的直角坐標方程;
(2)直線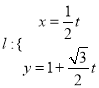 (
(![]() 為參數)與曲線
為參數)與曲線![]() 交于
交于![]() 兩點,與
兩點,與![]() 軸交于
軸交于![]() ,求
,求![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com