
【題目】樹立和踐行“綠水青山就是金山銀山,堅持人與自然和諧共生”的理念越來越深入人心,已形成了全民自覺參與,造福百姓的良性循環.據此,某網站退出了關于生態文明建設進展情況的調查,調查數據表明,環境治理和保護問題仍是百姓最為關心的熱點,參與調查者中關注此問題的約占![]() .現從參與關注生態文明建設的人群中隨機選出200人,并將這200人按年齡分組:第1組
.現從參與關注生態文明建設的人群中隨機選出200人,并將這200人按年齡分組:第1組![]() ,第2組
,第2組![]() ,第3組
,第3組![]() ,第4組
,第4組![]() ,第5組
,第5組![]() ,得到的頻率分布直方圖如圖所示.
,得到的頻率分布直方圖如圖所示.

(I)求出![]() 的值;
的值;
(II)求出這200人年齡的樣本平均數(同一組數據用該區間的中點值作代表)和中位數(精確到小數點后一位);
(III)現在要從年齡較小的第1,2組中用分層抽樣的方法抽取5人,再從這5人中隨機抽取3人進行問卷調查,求第2組恰好抽到2人的概率.
【答案】(1)0.035;(2)見解析;(3)見解析.
【解析】試題分析:(1)根據頻率分布直方圖的性質,各矩形的面積和為1,由此可算出![]() 的值,從而問題可得解;(2)在頻率分布直方中,數據樣本的平均數為各矩形的高與該組數據區間中點的乘積之和,中位數為使條形面積為0.5的橫坐標的值;(3)由頻率分布直方圖,可算出第1,2組的人數比,再根據古典概型概率的運算公式,從而問題可得解.
的值,從而問題可得解;(2)在頻率分布直方中,數據樣本的平均數為各矩形的高與該組數據區間中點的乘積之和,中位數為使條形面積為0.5的橫坐標的值;(3)由頻率分布直方圖,可算出第1,2組的人數比,再根據古典概型概率的運算公式,從而問題可得解.
試題解析:(1)由![]() ,得
,得![]() ,
,
(2)平均數為![]() 歲;
歲;
設中位數為![]() ,則
,則![]() ,∴
,∴![]() 歲.
歲.
(3)第1,2組抽取的人數分別為20人,30人,從第1,2組中用分層抽樣的方法抽取5人,則第1,2組抽取的人數分別為2人,3人,分別記為![]() .
.
設從5人中隨機抽取3人,為(![]() ),(
),(![]() ),(
),(![]() ),(
),(![]() ),(
),(![]() ),(
),(![]() ),(
),(![]() ),(
),(![]() ),(
),(![]() ),(
),(![]() ),共10個基本事件,
),共10個基本事件,
其中第2組恰好抽到2人包含(![]() ),(
),(![]() ),(
),(![]() ),(
),(![]() ),(
),(![]() ),(
),(![]() )共6個基本事件
)共6個基本事件
從而第2組抽到2人的概率![]()


 名師點睛字詞句段篇系列答案
名師點睛字詞句段篇系列答案科目:高中數學 來源: 題型:
【題目】(12分)
如圖,在四棱錐![]()
![]() .
.
(1)當PB=2時,證明:平面![]() 平面ABCD.
平面ABCD.
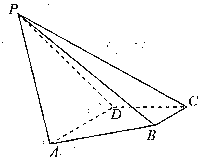 (2)當四棱錐
(2)當四棱錐![]() 的體積為
的體積為![]() ,且二面角
,且二面角![]() 為鈍角時,求直線PA與平面PCD所成角的正弦值.
為鈍角時,求直線PA與平面PCD所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4-4:坐標系與參數方程](10分)
在極坐標系中,圓C的極坐標方程為![]() ,若以極點O為原點,極軸為x軸的正半軸建立平面直角坐標系.
,若以極點O為原點,極軸為x軸的正半軸建立平面直角坐標系.
(1)求圓C的一個參數方程;
(2)在平面直角坐標系中,![]() 是圓C上的動點,試求
是圓C上的動點,試求![]() 的最大值,并求出此時點P的直角坐標.
的最大值,并求出此時點P的直角坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校將甲、乙等6名新招聘的老師分配到4個不同的年級,每個年級至少分配1名教師,且甲、乙兩名老師必須分到同一個年級,則不同的分法種數為______
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某社區組織“學習強國”的知識競賽,從參加競賽的市民中抽出40人,將其成績分成以下6組:第1組![]() ,第2組
,第2組![]() ,第3組
,第3組![]() ,第4組
,第4組![]() ,第5組
,第5組![]() ,第6組
,第6組![]() ,得到如圖所示的頻率分布直方圖.現采用分層抽樣的方法,從第2,3,4組中按分層抽樣抽取8人,則第2,3,4組抽取的人數依次為( )
,得到如圖所示的頻率分布直方圖.現采用分層抽樣的方法,從第2,3,4組中按分層抽樣抽取8人,則第2,3,4組抽取的人數依次為( )
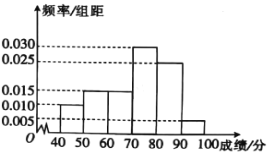
A.1,3,4B.2,3,3C.2,2,4D.1,1,6
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來,“共享單車”的出現為市民“綠色出行”提供了極大的方便,某共享單車公司計劃在甲、乙兩座城市共投資240萬元,根據行業規定,每個城市至少要投資80萬元,由前期市場調研可知:甲城市收益![]() 與投入
與投入![]() (單位:萬元)滿足
(單位:萬元)滿足![]() ,乙城市收益
,乙城市收益![]() 與投入
與投入![]() (單位:萬元)滿足
(單位:萬元)滿足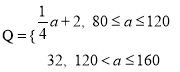 ,設甲城市的投入為
,設甲城市的投入為![]() (單位:萬元),兩個城市的總收益為
(單位:萬元),兩個城市的總收益為![]() (單位:萬元).
(單位:萬元).
(1)當投資甲城市128萬元時,求此時公司總收益;
⑵試問如何安排甲、乙兩個城市的投資,才能使公司總收益最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 滿足
滿足![]() ,
,![]() ,
,![]() 是數列
是數列![]() 的前
的前![]() 項的和.
項的和.
(1)求數列![]() 的通項公式;
的通項公式;
(2)若![]() ,
,![]() ,
,![]() 成等差數列,
成等差數列,![]() ,18,
,18,![]() 成等比數列,求正整數
成等比數列,求正整數![]() 的值;
的值;
(3)是否存在![]() ,使得
,使得![]() 為數列
為數列![]() 中的項?若存在,求出所有滿足條件的
中的項?若存在,求出所有滿足條件的![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,已知圓![]() 的方程為
的方程為![]() ,圓
,圓![]() 的方程為
的方程為![]() ,動圓
,動圓![]() 與圓
與圓![]() 內切且與圓
內切且與圓![]() 外切.
外切.
(1)求動圓圓心![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)已知![]() 與
與![]() 為平面內的兩個定點,過
為平面內的兩個定點,過![]() 點的直線
點的直線![]() 與軌跡
與軌跡![]() 交于
交于![]() ,
,![]() 兩點,求四邊形
兩點,求四邊形![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com