
【題目】已知四棱錐![]() 中,底面
中,底面![]() 是直角梯形,
是直角梯形,![]() ∥
∥![]() ,
,![]() ,
,![]() ,
,![]() ,又
,又![]() 平面
平面![]() ,且
,且![]() ,點
,點![]() 在棱
在棱![]() 上且
上且![]() .
.

(1)求證:![]() ;
;
(2)求![]() 與平面
與平面![]() 所成角的正弦值;
所成角的正弦值;
(3)求二面角![]() 的大小.
的大小.
【答案】(1)答案見解析(2)![]() (3)
(3)![]()
【解析】
(1)推導出![]() ,從而
,從而![]()
![]() 平面
平面![]() ,進而
,進而![]() ,由此能證明
,由此能證明![]()
![]() 平面
平面![]() ,即可求得答案;
,即可求得答案;
(2)由(1)可得:![]() 平面
平面![]() ,所以
,所以![]() 為
為![]() 與平面
與平面![]() 所成角,求出
所成角,求出![]() 長,即可求得答案;
長,即可求得答案;
(3)連結![]() ,交
,交![]() 于點
于點![]() ,
,![]() ,從而平面
,從而平面![]()
![]() 平面
平面![]() ,進而
,進而![]()
![]() 平面
平面![]() ,過
,過![]() 作
作![]()
![]()
![]() 于點
于點![]() ,連結
,連結![]() ,則
,則![]()
![]()
![]() ,則
,則![]() 為二面角
為二面角![]() 的平面角,即可求得答案.
的平面角,即可求得答案.
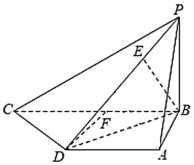
(1)取![]() 中點為
中點為![]() ,連接
,連接![]()
![]()
![]() ,
,
![]()
![]()
![]() 底面
底面![]() 是直角梯形,
是直角梯形,
![]()
![]() ∥
∥![]() ,即
,即![]() ∥
∥![]()
又![]()
![]()
![]() 四邊形
四邊形![]() 是平行四邊形
是平行四邊形
![]()
![]()
可得![]() ,
,![]() 中點為
中點為![]() ,
,
根據直角三角形性質可得:![]() 為直角三角形,且
為直角三角形,且![]()
![]()
![]()
又![]()
![]() 平面
平面![]()
![]()
![]()
![]() 平面
平面![]()
![]()
![]()
![]() 平面
平面![]()
![]()
(2)由(1)可得:![]() 平面
平面![]()
![]()
![]() 為
為![]() 與平面
與平面![]() 所成角
所成角
![]()
![]() 為直角三角形,
為直角三角形,![]() ,
,
又![]()
![]() ,
,![]()
![]()
![]() 為等腰直角三角形
為等腰直角三角形
![]()
![]()
在![]() 中,
中,![]()
![]()
![]()
![]()
![]() 與平面
與平面![]() 所成角的正弦值
所成角的正弦值![]() .
.
(3)連結![]() ,交
,交![]() 于點
于點![]() ,
,![]() ,如圖:
,如圖:

![]()
![]() 平面
平面![]() ,
,
![]() 平面
平面![]()
![]() 平面
平面![]() ,
,
![]()
![]()
![]() 平面
平面![]()
過![]() 作
作![]()
![]()
![]() 于點
于點![]() ,連結
,連結![]() ,則
,則![]()
![]()
![]() ,
,
![]()
![]() 為二面角
為二面角![]() 的平面角,
的平面角,
在![]() 中,
中,![]()
在![]() 中,
中,![]()
在![]() 中,
中,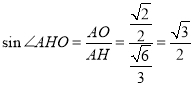
![]()
![]() 二面角
二面角![]() 的大小為
的大小為![]() .
.


 小學教材完全解讀系列答案
小學教材完全解讀系列答案科目:高中數學 來源: 題型:
【題目】在△ABC中“sinA>sinB”是“cosA<cosB”的( )
A.充分不必要條件 B.必要不充分條件
C.充要條件 D.既不充分也不必要條件
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國是水資源匱乏國家,節約用水是每個中國公民應有的意識.為了保護水資源,提倡節約用水,某城市對居民生活用水實行“階梯水價”,計費方法如下表:
每戶每月用水量 | 水價 |
不超過12 | 3元/ |
超過12 | 6元/ |
超過18 | 9元/ |
(1)該城市居民小張家月用水量記為![]() ,應交納水費y(元),試建立y與x的函數解析式,并作出其圖像;
,應交納水費y(元),試建立y與x的函數解析式,并作出其圖像;
(2)若小張家十月份交納水費90元,求他家十月份的用水量.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)當![]() 時,解不等式
時,解不等式![]() ;
;
(2)若關于![]() 的方程
的方程![]() 在區間
在區間![]() 上恰有一個實數解,求
上恰有一個實數解,求![]() 的取值范圍;
的取值范圍;
(3)設![]() ,若存在
,若存在![]() 使得函數
使得函數![]() 在區間
在區間![]() 上的最大值和最小值的差不超過1,求
上的最大值和最小值的差不超過1,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定點M(0,2),N(-2,0),直線l:kx-y-2k+2=0(k為常數).
(1)若點M,N到直線l的距離相等,求實數k的值;
(2)對于l上任意一點P,∠MPN恒為銳角,求實數k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校有1200名學生,隨機抽出300名進行調查研究,調查者設計了一個隨機化裝置,這是一個裝有大小、形狀和質量完全相同的10個紅球,10個綠球和10個白球的袋子.調查中有兩個問題:
問題1:你的陽歷生日月份是不是奇數?
問題2:你是否抽煙?
每個被調查者隨機從袋中摸出1個球(摸出后再放回袋中).若摸到紅球就如實回答第一個問題,若摸到綠球,則不回答任何問題;若摸到白球,則如實回答第二個問題.所有回答“是”的調查者只需往一個盒子中放一個小石子,回答“否”的被調查者什么也不用做.最后收集回來53個小石子,估計該學校吸煙的人數有多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐![]() 中,底面ABCD為矩形,點E在線段PA上,
中,底面ABCD為矩形,點E在線段PA上,![]() 平面BDE.
平面BDE.
![]() 求證:
求證:![]() ;
;
![]() 若
若![]() 是等邊三角形,
是等邊三角形,![]() ,平面
,平面![]() 平面ABCD,四棱錐
平面ABCD,四棱錐![]() 的體積為
的體積為![]() ,求點E到平面PCD的距離.
,求點E到平面PCD的距離.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于函數![]() ,若存在實數對
,若存在實數對![]() ,使得等式
,使得等式![]() 對定義域中的任意
對定義域中的任意![]() 都成立,則稱函數
都成立,則稱函數![]() 是“
是“![]() 型函數”.
型函數”.
(1)若函數![]() 是“
是“![]() 型函數”,且
型函數”,且![]() ,求出滿足條件的實數對
,求出滿足條件的實數對![]() ;
;
(2)已知函數![]() .函數
.函數![]() 是“
是“![]() 型函數”,對應的實數對
型函數”,對應的實數對![]() 為
為![]() ,當
,當![]() 時,
時,![]() .若對任意
.若對任意![]() 時,都存在
時,都存在![]() ,使得
,使得![]() ,試求
,試求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com