
【題目】設橢圓![]() 的離心率為
的離心率為![]() ,左頂點到直線
,左頂點到直線![]() 的距離為
的距離為![]() .
.
(Ⅰ)求橢圓C的方程;
(Ⅱ)設直線![]() 與橢圓C相交于A、B兩點,若以AB為直徑的圓經過坐標原點O,試探究:點O到直線AB的距離是否為定值?若是,求出這個定值;否則,請說明理由;
與橢圓C相交于A、B兩點,若以AB為直徑的圓經過坐標原點O,試探究:點O到直線AB的距離是否為定值?若是,求出這個定值;否則,請說明理由;
(Ⅲ)在(Ⅱ)的條件下,試求△AOB面積S的最小值.
【答案】(1)![]() (2)見解析;(3)
(2)見解析;(3)![]()
【解析】
(Ⅰ)由已知,根據點到直線的距離公式,求解![]() ,再由橢圓的離心率,求得
,再由橢圓的離心率,求得![]() ,進而可求得橢圓的方程;
,進而可求得橢圓的方程;
(Ⅱ)法一:設![]() ,
,![]() ,①當直線l的斜率不存在時,求得點O到直線AB的距離為定值;②當直線l的斜率存在時,設其方程為
,①當直線l的斜率不存在時,求得點O到直線AB的距離為定值;②當直線l的斜率存在時,設其方程為![]() 聯立方程組,根據根與系數的關系和題設條件,化簡得
聯立方程組,根據根與系數的關系和題設條件,化簡得![]() ,進而求得點O到直線AB的距離為定值.
,進而求得點O到直線AB的距離為定值.
法二:設直線方程為![]() ,聯立方程組,利用根與系數的關系和題設條件,化簡得
,聯立方程組,利用根與系數的關系和題設條件,化簡得![]() ,進而得到點O到直線AB的距離為定值;
,進而得到點O到直線AB的距離為定值;
(Ⅲ)法一:當直線OA、直線OB斜率存在且不為0時,設直線OA的斜率為k,聯立方程組,進而求得面積的表達式,利用基本不等式,即可求解面積的最小值;
法二:由(Ⅱ),①當直線l的斜率不存在時,![]() ,②當直線l的斜率存在時,得出面積的表示,利用基本不等式求得最小值,即可得到答案.
,②當直線l的斜率存在時,得出面積的表示,利用基本不等式求得最小值,即可得到答案.
(Ⅰ)由已知,![]() )
)
因為![]() 故所求橢圓的方程為
故所求橢圓的方程為![]() ;
;
(Ⅱ)法一:設![]() ,
,![]() ,
,
①當直線l的斜率不存在時,由橢圓對稱性知![]() ,
,![]() ,因為以AB為直徑的圓經過坐標原點O,故
,因為以AB為直徑的圓經過坐標原點O,故![]() ,即
,即![]()
又因為點![]() 在橢圓上,故
在橢圓上,故![]() ,解得
,解得![]() ,
,
此時點O到直線AB的距離為![]()
②當直線l的斜率存在時,設其方程為![]() .
.
聯立![]() 得:
得:![]()
所以![]() ,
,
由已知,以AB為直徑的圓經過坐標原點O,則![]() ,且
,且![]()
故![]()
化簡得![]() ,
,
故點O到直線AB的距離為![]() 綜上,點O到直線AB的距離為定值
綜上,點O到直線AB的距離為定值![]()
法二:(若設直線方程為![]() ,也要對直線斜率為0進行討論)
,也要對直線斜率為0進行討論)
設![]() ,
,
①當直線l的斜率為0時,由橢圓對稱性知x1=-x2,y1=y2,因為以AB為直徑的圓經過坐標原點O,故![]() ,即
,即![]()
又因為點![]() 在橢圓上,故
在橢圓上,故![]() ,解得
,解得![]() ,
,
此時點O到直線AB的距離為![]()
②當直線l的斜率不為0,或斜率不存在時,設其方程為![]() .
.
聯立![]() 得:
得:![]()
所以![]() ,
,
故![]() ,
,
即![]() ,所以
,所以![]() ,
,
所以![]() ,
,
化簡得![]() ,故點O到直線AB的距離為
,故點O到直線AB的距離為![]()
綜上,點O到直線AB的距離為定值![]()
(Ⅲ)法一:當直線OA、直線OB中有一條斜率不存在,另一條斜率為0時,易知S=1;
當直線OA、直線OB斜率存在且不為0時,設直線OA的斜率為k,
則直線OB的斜率為![]() ,由
,由![]() 得
得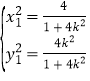 ,
,
同理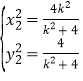 故
故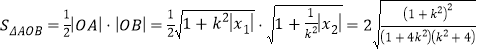
令![]() ,則
,則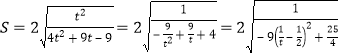
故![]() 綜上,△AOB面積S的最小值為
綜上,△AOB面積S的最小值為![]() .
.
法二:由(Ⅱ),①當直線l的斜率不存在時,![]() ,
,
②當直線l的斜率存在時,![]() ,且點O到直線AB的距離為
,且點O到直線AB的距離為![]() ,
,
![]()
![]()
故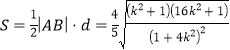 ,
,
令![]() ,則
,則![]() ,
,
因為![]() ,故
,故![]() .綜上,△AOB面積S的最小值為
.綜上,△AOB面積S的最小值為![]() .
.


科目:高中數學 來源: 題型:
【題目】如圖,已知圓![]() 與
與![]() 軸的左右交點分別為
軸的左右交點分別為![]() ,與
,與![]() 軸正半軸的交點為
軸正半軸的交點為![]() .
.
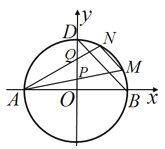
(1)若直線![]() 過點
過點![]() 并且與圓
并且與圓![]() 相切,求直線
相切,求直線![]() 的方程;
的方程;
(2)若點![]() 是圓
是圓![]() 上第一象限內的點,直線
上第一象限內的點,直線![]() 分別與
分別與![]() 軸交于點
軸交于點![]() ,點
,點![]() 是線段
是線段![]() 的中點,直線
的中點,直線![]() ,求直線
,求直線![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】關于函數![]() 有如下命題:
有如下命題:
①![]() ; ②函數的圖象關于原點中心對稱;
; ②函數的圖象關于原點中心對稱;
③函數的定義域與值域相同; ④函數的圖象必經過第二、四象限.
其中正確命題的個數是( )
A.4B.3C.2D.1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() (
(![]() )的離心率為
)的離心率為![]() ,短軸端點到焦點的距離為
,短軸端點到焦點的距離為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設![]() ,
,![]() 為橢圓
為橢圓![]() 上任意兩點,
上任意兩點,![]() 為坐標原點,且
為坐標原點,且![]() .求證:原點
.求證:原點![]() 到直線
到直線![]() 的距離為定值,并求出該定值.
的距離為定值,并求出該定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2017年是某市大力推進居民生活垃圾分類的關鍵一年,有關部門為宣傳垃圾分類知識,面向該市市民進行了一次“垃圾分類知識”的網絡問卷調查,每位市民僅有一次參與機會,通過抽樣,得到參與問卷調查中的1000人的得分數據,其頻率分布直方圖如圖所示:
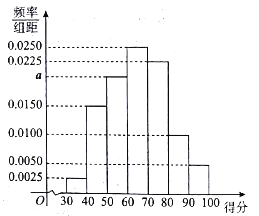
(1)估計該組數據的中位數、眾數;
(2)由頻率分布直方圖可以認為,此次問卷調查的得分![]() 服從正態分布
服從正態分布![]() ,
, ![]() 近似為這1000人得分的平均值(同一組數據用該區間的中點值作代表),利用該正態分布,求
近似為這1000人得分的平均值(同一組數據用該區間的中點值作代表),利用該正態分布,求![]() ;
;
(3)在(2)的條件下,有關部門為此次參加問卷調查的市民制定如下獎勵方案:
(ⅰ)得分不低于![]() 可獲贈2次隨機話費,得分低于
可獲贈2次隨機話費,得分低于![]() 則只有1次;
則只有1次;
(ⅱ)每次贈送的隨機話費和對應概率如下:

現有一位市民要參加此次問卷調查,記![]() (單位:元)為該市民參加問卷調查獲贈的話費,求
(單位:元)為該市民參加問卷調查獲贈的話費,求![]() 的分布列和數學期望.
的分布列和數學期望.
附: ![]() ,
,
若![]() ,則
,則![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某小區中央廣場由兩部分組成,一部分是邊長為![]() 的正方形
的正方形![]() ,另一部分是以
,另一部分是以![]() 為直徑的半圓,其圓心為
為直徑的半圓,其圓心為![]() .規劃修建的
.規劃修建的![]() 條直道
條直道![]() ,
, ![]() ,
, ![]() 將廣場分割為
將廣場分割為![]() 個區域:Ⅰ、Ⅲ、Ⅴ為綠化區域(圖中陰影部分),Ⅱ、Ⅳ、Ⅵ為休閑區域,其中點
個區域:Ⅰ、Ⅲ、Ⅴ為綠化區域(圖中陰影部分),Ⅱ、Ⅳ、Ⅵ為休閑區域,其中點![]() 在半圓弧上,
在半圓弧上, ![]() 分別與
分別與![]() ,
, ![]() 相交于點
相交于點![]() ,
, ![]() .(道路寬度忽略不計)
.(道路寬度忽略不計)
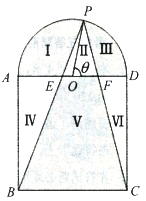
(1)若![]() 經過圓心,求點
經過圓心,求點![]() 到
到![]() 的距離;
的距離;
(2)設![]() ,
, ![]() .
.
①試用![]() 表示
表示![]() 的長度;
的長度;
②當![]() 為何值時,綠化區域面積之和最大.
為何值時,綠化區域面積之和最大.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com