
【題目】已知圓C的圓心為(1,1),直線![]() 與圓C相切.
與圓C相切.
(1)求圓C的標準方程;
(2)若直線過點(2,3),且被圓C所截得的弦長為2,求直線的方程.
 學練快車道口算心算速算天天練系列答案
學練快車道口算心算速算天天練系列答案科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]()
![]() ,點P為直線l:
,點P為直線l:![]() 上且不在x軸上的任意一點,直線
上且不在x軸上的任意一點,直線![]() 和
和![]() 與橢圓的交點分別為A、B和C、D、O為坐標原點.
與橢圓的交點分別為A、B和C、D、O為坐標原點.
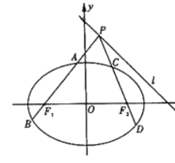
(1)求![]() 的周長;
的周長;
(2)設(shè)直線![]()
![]() 的斜線分別為
的斜線分別為![]()
![]() ,證明:
,證明:![]() ;
;
(3)問直線l上是否存在點P,使得直線OA、OB、OC、OD的斜率![]() 滿足
滿足![]() ?若存在,求出所有滿足條件的點P的坐標;若不存在,說明理由.
?若存在,求出所有滿足條件的點P的坐標;若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某企業(yè)為了檢查生產(chǎn)![]() 產(chǎn)品的甲、乙兩條流水線的生產(chǎn)情況,隨機地從這兩條流水線上生產(chǎn)的大量產(chǎn)品中各抽取50件產(chǎn)品作為樣本,測出它們的這一項質(zhì)量指標值.若該項質(zhì)量指標值落在
產(chǎn)品的甲、乙兩條流水線的生產(chǎn)情況,隨機地從這兩條流水線上生產(chǎn)的大量產(chǎn)品中各抽取50件產(chǎn)品作為樣本,測出它們的這一項質(zhì)量指標值.若該項質(zhì)量指標值落在![]() 內(nèi),則為合格品,否則為不合格品.下表是甲流水線樣本的頻數(shù)分布表,下圖是乙流水線樣本的頻率分布直方圖.
內(nèi),則為合格品,否則為不合格品.下表是甲流水線樣本的頻數(shù)分布表,下圖是乙流水線樣本的頻率分布直方圖.
甲流水線樣本的頻數(shù)分布表
質(zhì)量指標值 | 頻數(shù) |
| 9 |
| 10 |
| 17 |
| 8 |
| 6 |
乙流水線樣本的頻率分布直方圖
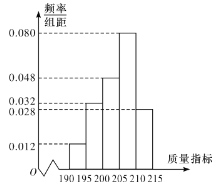
(1)根據(jù)圖形,估計乙流水線生產(chǎn)的![]() 產(chǎn)品的該項質(zhì)量指標值的中位數(shù);
產(chǎn)品的該項質(zhì)量指標值的中位數(shù);
(2)設(shè)該企業(yè)生產(chǎn)一件合格品獲利100元,生產(chǎn)一件不合格品虧損50元,若某個月內(nèi)甲、乙兩條流水線均生產(chǎn)了1000件產(chǎn)品,若將頻率視為概率,則該企業(yè)本月的利潤約為多少元?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】我們要計算由拋物線![]() ,x軸以及直線
,x軸以及直線![]() 所圍成的區(qū)域的面積S,可用x軸上的分點
所圍成的區(qū)域的面積S,可用x軸上的分點![]() 、
、![]() 、
、![]() 、…、
、…、![]() 、1將區(qū)間
、1將區(qū)間![]() 分成n個小區(qū)間,在每個小區(qū)間上做一個小矩形,使矩形的左端點在拋物線
分成n個小區(qū)間,在每個小區(qū)間上做一個小矩形,使矩形的左端點在拋物線![]() 上,這些矩形的高分別為
上,這些矩形的高分別為![]() 、
、![]() 、
、![]() 、…、
、…、![]() ,矩形的底邊長都是
,矩形的底邊長都是![]() ,設(shè)所有這些矩形面積的總和為
,設(shè)所有這些矩形面積的總和為![]() ,為求S,只須令分割的份數(shù)n無限增大,
,為求S,只須令分割的份數(shù)n無限增大,![]() 就無限趨近于S,即
就無限趨近于S,即![]() .
.
(1)求數(shù)列![]() 的通項公式,并求出S;
的通項公式,并求出S;
(2)利用相同的思想方法,探求由函數(shù)![]()
![]() 的圖象,x軸以及直線
的圖象,x軸以及直線![]() 和
和![]() 所圍成的區(qū)域的面積T.
所圍成的區(qū)域的面積T.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】“勾股定理”在西方被稱為“畢達哥拉斯定理”,國時期吳國的數(shù)學家趙爽創(chuàng)制了一幅“勾股圓方圖”,用數(shù)形結(jié)合的方法給出了勾股定理的詳細證明![]() 如圖所示的“勾股圓方圖”中,四個相同的直角三角形與中間的小正方形拼成一個大正方形
如圖所示的“勾股圓方圖”中,四個相同的直角三角形與中間的小正方形拼成一個大正方形![]() 若直角三角形中較小的銳角
若直角三角形中較小的銳角![]() ,現(xiàn)在向該大止方形區(qū)域內(nèi)隨機地投擲一枚飛鏢,則飛鏢落在陰影部分的概率是
,現(xiàn)在向該大止方形區(qū)域內(nèi)隨機地投擲一枚飛鏢,則飛鏢落在陰影部分的概率是![]()
![]()

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】下列命題中正確的是( )
A.若無窮數(shù)列![]() 單調(diào)遞增,則數(shù)列
單調(diào)遞增,則數(shù)列![]() 的極限存在
的極限存在
B.數(shù)列![]() 的一個極限值為0
的一個極限值為0
C.若存在常數(shù)![]() ,使得
,使得![]() 恒成立,則無窮數(shù)列
恒成立,則無窮數(shù)列![]() 的極限存在
的極限存在
D.若無窮數(shù)列![]() 的極限存在,則存在常數(shù)
的極限存在,則存在常數(shù)![]() ,使得
,使得![]() 恒成立
恒成立
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某高校在![]() 年的自主招生考試成績中隨機抽取
年的自主招生考試成績中隨機抽取![]() 名學生的筆試成績,按成績分組:第
名學生的筆試成績,按成績分組:第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() 得到的頻率分布直方圖如圖所示
得到的頻率分布直方圖如圖所示
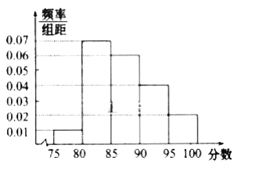
![]() 分別求第
分別求第![]() 組的頻率;
組的頻率;
![]() 若該校決定在第
若該校決定在第![]() 組中用分層抽樣的方法抽取
組中用分層抽樣的方法抽取![]() 名學生進入第二輪面試,
名學生進入第二輪面試,
![]() 已知學生甲和學生乙的成績均在第
已知學生甲和學生乙的成績均在第![]() 組,求學生甲和學生乙同時進入第二輪面試的概率;
組,求學生甲和學生乙同時進入第二輪面試的概率;
![]() 根據(jù)直方圖試估計這
根據(jù)直方圖試估計這![]() 名學生成績的平均分.(同一組中的數(shù)據(jù)用改組區(qū)間的中間值代表)
名學生成績的平均分.(同一組中的數(shù)據(jù)用改組區(qū)間的中間值代表)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() 的導函數(shù)為
的導函數(shù)為![]() .
.
(1)試討論函數(shù)![]() 的零點個數(shù);
的零點個數(shù);
(2)若對任意的![]() ,關(guān)于
,關(guān)于![]() 的不等式
的不等式![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com