
【題目】某城市理論預測2007年到2011年人口總數與年份的關系如表所示
年份2007+x(年) | 0 | 1 | 2 | 3 | 4 |
人口數y(十萬) | 5 | 7 | 8 | 11 | 19 |
(1)請根據表提供的數據,求最小二乘法求出y關于x的線性回歸方程;
(2)據此估計2012年該城市人口總數.
參考公式: 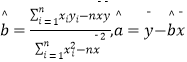 .
.
科目:高中數學 來源: 題型:
【題目】定義在R上的奇函數f(x),當x∈(﹣∞,0)時,f(x)=﹣x2+mx﹣1.
(1)求f(x)的解析式;
(2)若方程f(x)=0有五個不相等的實數解,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列![]() 是各項均為正數的等比數列,其前
是各項均為正數的等比數列,其前![]() 項和為
項和為![]() ,且
,且![]() .
.
(1)求數列![]() 的通項公式;
的通項公式;
(2)設有正整數![]() ,使得
,使得![]() 成等差數列,求
成等差數列,求![]() 的值;
的值;
(3)設![]() ,對于給定的
,對于給定的![]() ,求三個數
,求三個數![]() 經適當排序后能構成等差數列的充要條件.
經適當排序后能構成等差數列的充要條件.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在等腰梯形ABCD中,AD∥BC,AB=DC,過點D作AC的平行線DE,交BA的延長線于點E.求證: 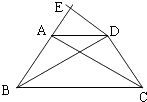
(1)△ABC≌△DCB;
(2)DEDC=AEBD.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() .
.
(1)若橢圓的離心率為![]() ,且點
,且點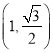 在橢圓上,①求橢圓的方程;
在橢圓上,①求橢圓的方程;
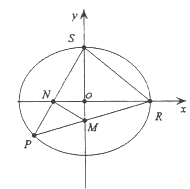
②設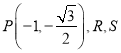 分別為橢圓
分別為橢圓![]() 的右頂點和上頂點,直線
的右頂點和上頂點,直線![]() 和
和![]() 與
與![]() 軸和
軸和![]() 軸相交于點
軸相交于點![]() ,求直線
,求直線![]() 的方程;
的方程;
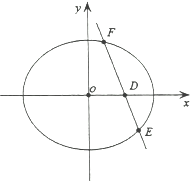
(2)設 ![]() 過
過![]() 點的直線
點的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點,且
兩點,且![]() 均在
均在![]() 的右側,
的右側, ![]() ,求橢圓離心率的取值范圍.
,求橢圓離心率的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某汽車美容公司為吸引顧客,推出優惠活動:對首次消費的顧客,按![]() 元/次收費, 并注冊成為會員, 對會員逐次消費給予相應優惠,標準如下:
元/次收費, 并注冊成為會員, 對會員逐次消費給予相應優惠,標準如下:
消費次第 | 第 | 第 | 第 | 第 |
|
收費比例 |
|
|
|
|
|
該公司從注冊的會員中, 隨機抽取了![]() 位進行統計, 得到統計數據如下:
位進行統計, 得到統計數據如下:
消費次第 | 第 | 第 | 第 | 第 | 第 |
頻數 |
|
|
|
|
|
假設汽車美容一次, 公司成本為![]() 元, 根據所給數據, 解答下列問題:
元, 根據所給數據, 解答下列問題:
(1)估計該公司一位會員至少消費兩次的概率;
(2)某會員僅消費兩次, 求這兩次消費中, 公司獲得的平均利潤;
(3)以事件發生的頻率作為相應事件發生的概率, 設該公司為一位會員服務的平均利潤為![]() 元, 求
元, 求![]() 的分布列和數學期望
的分布列和數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校從參加高三化學得分訓練的學生中隨機抽出60名學生,將其化學成績(均為整數)分成六段![]() 、
、![]() 、…、
、…、![]() 后得到部分頻率分布直方圖(如圖).
后得到部分頻率分布直方圖(如圖).
觀察圖形中的信息,回答下列問題:
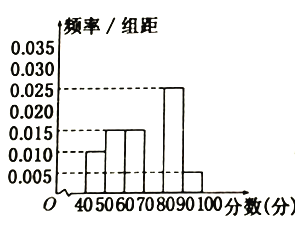
(1)求分數在![]() 內的頻率,并補全頻率分布直方圖;
內的頻率,并補全頻率分布直方圖;
(2)據此估計本次考試的平均分;
(3)若從60名學生中隨機抽取2人,抽到的學生成績在![]() 內記0分,在
內記0分,在![]() 內記1分,在
內記1分,在![]() 內記2分,用
內記2分,用![]() 表示抽取結束后的總記分,求
表示抽取結束后的總記分,求![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義在R上的函數f(x)=2|x﹣m|﹣1(m為實數)為偶函數,記a=f(log0.53),b=f(log25),c=f(2m),則a,b,c的大小關系為 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com