
【題目】如圖,矩形ABCD中,![]() ,
,![]() ,E,F分別為AD,AB中點,M為線段BC上的一個動點,現將
,E,F分別為AD,AB中點,M為線段BC上的一個動點,現將![]() ,
,![]() ,分別沿EC,EF折起,使A,D重合于點P.設PM與平面BCEF所成角為
,分別沿EC,EF折起,使A,D重合于點P.設PM與平面BCEF所成角為![]() ,二面角
,二面角![]() 的平面角為
的平面角為![]() ,二面角
,二面角![]() 的平面角為
的平面角為![]() ,則( )
,則( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
過![]() 作
作![]()
![]() 平面
平面![]() ,作出三個二面角
,作出三個二面角![]() ,二面角
,二面角![]() 的平面角,二面角
的平面角,二面角![]() 的平面角,通過原平面圖形計算可得這三個角的大小關系.從而得出結論.
的平面角,通過原平面圖形計算可得這三個角的大小關系.從而得出結論.
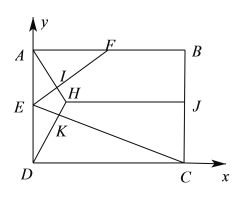
在![]() 翻折過程中,A點在底面的投影在過點A且垂直EF的直線上(設垂足為I),同理在
翻折過程中,A點在底面的投影在過點A且垂直EF的直線上(設垂足為I),同理在![]() 翻折過程中,D點在底面的投影在過點D且垂直EC的直線上(設垂足為K),設點P在底面的投影為點H,過點H向BC作垂線HJ(垂足為J),
翻折過程中,D點在底面的投影在過點D且垂直EC的直線上(設垂足為K),設點P在底面的投影為點H,過點H向BC作垂線HJ(垂足為J),
把![]() ,
,![]() 攤平到原來的平面圖形,如下右圖,
攤平到原來的平面圖形,如下右圖,![]() 就是
就是![]() 和
和![]() 延長線的交點,由已知可得
延長線的交點,由已知可得![]() ,
,![]() ,
,![]() ,則
,則![]() ,
,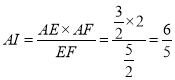 ,同理可得
,同理可得![]() ,
,![]() ,則在左圖中知易得
,則在左圖中知易得![]() ,由二面角的定義知
,由二面角的定義知![]() ,所以
,所以![]() ,
,
又在右圖中,以![]() ,
,![]() 為
為![]() 軸建立平面直角坐標系,
軸建立平面直角坐標系,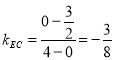 ,則
,則![]() ,直線
,直線![]() 方程為
方程為![]() ,同理直線
,同理直線![]() 的方程為
的方程為![]() ,由
,由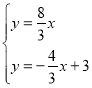 得
得![]() ,即
,即![]() ,∴
,∴![]() ,∴
,∴![]() ,所以二面角
,所以二面角![]() 的平面角小于二面角
的平面角小于二面角![]() 的平面角,顯然
的平面角,顯然![]() 不大于二面角
不大于二面角![]() 的平面角,∴
的平面角,∴![]() ,綜上可知
,綜上可知![]() ,
,
故選:D



 津橋教育計算小狀元系列答案
津橋教育計算小狀元系列答案科目:高中數學 來源: 題型:
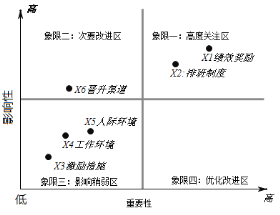
【題目】2020年1月,某公司以問卷的形式調查影響員工積極性的六項關鍵指標:績效獎勵、排班制度、激勵措施、工作環境、人際關系、晉升渠道,在確定各項指標權重結果后,進而得到指標重要性分析象限圖(如圖).若客戶服務中心從中任意抽取不同的兩項進行分析,則這兩項來自影響稍弱區的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以直角坐標系的原點為極點,![]() 軸的非負半軸為極軸建立極坐標系,曲線
軸的非負半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,直線
,直線![]() 的參數方程為
的參數方程為 (
(![]() 為參數).
為參數).
(1)求曲線![]() 的參數方程與直線
的參數方程與直線![]() 的普通方程;
的普通方程;
(2)設點過![]() 為曲線
為曲線![]() 上的動點,點
上的動點,點![]() 和點
和點![]() 為直線
為直線![]() 上的點,且滿足
上的點,且滿足![]() 為等邊三角形,求
為等邊三角形,求![]() 邊長的取值范圍.
邊長的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分圖象如圖所示,又函數![]() .
.
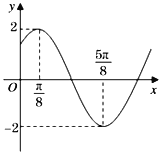
(1)求函數![]() 的單調減區間;
的單調減區間;
(2)設△ABC的內角A,B,C的對邊分別為a,b,c,又![]() ,且銳角C滿足
,且銳角C滿足![]() ,若sinB=2sinA,求a+b的值.
,若sinB=2sinA,求a+b的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國是世界嚴重缺水的國家,城市缺水問題較為突出,某市政府為了鼓勵居民節約用水,計劃在本市試行居民生活用水定額管理,即確定一個合理的居民月用水量標準![]() (噸),用水量不超過
(噸),用水量不超過![]() 的部分按平價收費,超過
的部分按平價收費,超過![]() 的部分按議價收費,為了了解全市民月用水量的分布情況,通過抽樣,獲得了100位居民某年的月用水量(單位:噸),將數據按照
的部分按議價收費,為了了解全市民月用水量的分布情況,通過抽樣,獲得了100位居民某年的月用水量(單位:噸),將數據按照![]() 分成9組,制成了如圖所示的頻率分布直方圖.
分成9組,制成了如圖所示的頻率分布直方圖.

(Ⅰ)若全市居民中月均用水量不低于3噸的人數為3.6萬,試估計全市有多少居民?并說明理由;
(Ⅱ)若該市政府擬采取分層抽樣的方法在用水量噸數為![]() 和
和![]() 之間選取7戶居民作為議價水費價格聽證會的代表,并決定會后從這7戶家庭中按抽簽方式選出4戶頒發“低碳環保家庭”獎,設
之間選取7戶居民作為議價水費價格聽證會的代表,并決定會后從這7戶家庭中按抽簽方式選出4戶頒發“低碳環保家庭”獎,設![]() 為用水量噸數在
為用水量噸數在![]() 中的獲獎的家庭數,
中的獲獎的家庭數,![]() 為用水量噸數在
為用水量噸數在![]() 中的獲獎家庭數,記隨機變量
中的獲獎家庭數,記隨機變量![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在長方體ABCD﹣A1B1C1D1中,AA1=2AB=2AD=4,過AA1作平面α使BD⊥α,且平面α∩平面A1B1C1D1=l,M∈l.下面給出了四個命題:這四個命題中,真命題的個數為( )
①l∥AC;
②BM⊥AC;
③l和AD1所成的角為60°;
④線段BM長度的最小值為![]() .
.
A.1B.2C.3D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為比較甲,乙兩地某月![]() 時的氣溫,隨機選取該月中的
時的氣溫,隨機選取該月中的![]() 天,將這
天,將這![]() 天中
天中![]() 時的氣溫數據(單位:℃)制成如圖所示的莖葉圖,考慮以下結論:①甲地該月
時的氣溫數據(單位:℃)制成如圖所示的莖葉圖,考慮以下結論:①甲地該月![]() 時的平均氣溫低于乙地該月
時的平均氣溫低于乙地該月![]() 時的平均氣溫;②甲地該月
時的平均氣溫;②甲地該月![]() 時的平均氣溫高于乙地該月
時的平均氣溫高于乙地該月![]() 時的平均氣溫;③甲地該月
時的平均氣溫;③甲地該月![]() 時的氣溫的中位數小于乙地該月
時的氣溫的中位數小于乙地該月![]() 時的氣溫的中位數;④甲地該月
時的氣溫的中位數;④甲地該月![]() 時的氣溫的中位數大于乙地該月
時的氣溫的中位數大于乙地該月![]() 時的氣溫的中位數.其中根據莖葉圖能得到的正確結論的編號為( )
時的氣溫的中位數.其中根據莖葉圖能得到的正確結論的編號為( )

A. ①③ B. ①④ C. ②③ D. ②④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(1)某中學理學社為了吸收更多新社員,在校團委的支持下,在高一學年組織了抽簽贈書活動.月初報名,月末抽簽,最初有30名同學參加.社團活動積極分子甲同學參加了活動.
①第一個月有18個中簽名額.甲先抽簽,乙和丙緊隨其后抽簽.求這三名同學同時中簽的概率.
②理學社設置了第![]() (
(![]() )個月中簽的名額為
)個月中簽的名額為![]() ,并且抽中的同學退出活動,同時補充新同學,補充的同學比中簽的同學少2個,如果某次抽簽的同學全部中簽,則活動立刻結束.求甲同學參加活動時間的期望.
,并且抽中的同學退出活動,同時補充新同學,補充的同學比中簽的同學少2個,如果某次抽簽的同學全部中簽,則活動立刻結束.求甲同學參加活動時間的期望.
(2)某出版集團為了擴大影響,在全國組織了抽簽贈書活動.報名和抽簽時間與(1)中某中學理學社的報名和抽簽時間相同,最初有30萬人參加,甲同學在其中.每個月抽中的人退出活動,同時補充新人,補充的人數與中簽的人數相同.出版集團設置了第![]() (
(![]() )個月中簽的概率為
)個月中簽的概率為![]() ,活動進行了
,活動進行了![]() 個月,甲同學很幸運,中簽了,在此條件下,求證:甲同學參加活動時間的均值小于
個月,甲同學很幸運,中簽了,在此條件下,求證:甲同學參加活動時間的均值小于![]() 個月.
個月.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com