
【題目】不重合的兩條直線![]() ,
,![]() 和不重合的兩個平面
和不重合的兩個平面![]() ,
,![]() ,下面的幾個命題:①若
,下面的幾個命題:①若![]() ,且
,且![]() ,則
,則![]() ;②若
;②若![]() ,
,![]() 與平面
與平面![]() 成等角,則
成等角,則![]() ;③若
;③若![]() ,
,![]() ,且
,且![]() ,則
,則![]() ;④若
;④若![]() ,
,![]() ,則
,則![]() ;⑤若
;⑤若![]() ,
,![]() 異面,且
異面,且![]() ,
,![]() 均與平面
均與平面![]() 和
和![]() 平行,則
平行,則![]() .在這5個命題中,真命題的個數是( )
.在這5個命題中,真命題的個數是( )
A.1B.2C.3D.4
 手拉手全優練考卷系列答案
手拉手全優練考卷系列答案科目:高中數學 來源: 題型:
【題目】如圖,在正方體![]() 中,點
中,點![]() 是線段
是線段![]() 上的動點,則下列說法錯誤的是( )
上的動點,則下列說法錯誤的是( )
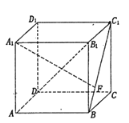
A. 當點![]() 移動至
移動至![]() 中點時,直線
中點時,直線![]() 與平面
與平面![]() 所成角最大且為
所成角最大且為![]()
B. 無論點![]() 在
在![]() 上怎么移動,都有
上怎么移動,都有![]()
C. 當點![]() 移動至
移動至![]() 中點時,才有
中點時,才有![]() 與
與![]() 相交于一點,記為點
相交于一點,記為點![]() ,且
,且![]()
D. 無論點![]() 在
在![]() 上怎么移動,異面直線
上怎么移動,異面直線![]() 與
與![]() 所成角都不可能是
所成角都不可能是![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】依照某發展中國家2018年的官方資料,將該國所有家庭按年收入從低到高的順序平均分為五組,依次為第一組至第五組,各組家庭的年收入總和占該國全部家庭的年收入總和的百分比如圖所示.
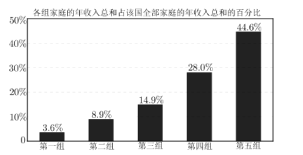
以下關于該國2018年家庭收入的判斷,一定正確的是( )
A. 至少有![]() 的家庭的年收入都低于全部家庭的平均年收入
的家庭的年收入都低于全部家庭的平均年收入
B. 收入最低的那![]() 的家庭平均年收入為全部家庭平均年收入的
的家庭平均年收入為全部家庭平均年收入的![]()
C. 收入最高的那![]() 的家庭年收入總和超過全部家庭年收入總和的
的家庭年收入總和超過全部家庭年收入總和的![]()
D. 收入最低的那![]() 的家庭年收入總和超過全部家庭年收入總和的
的家庭年收入總和超過全部家庭年收入總和的![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知在乎面直角坐標系![]() 中,直線
中,直線![]() :
:![]() (
(![]() 為參數),以原點為極點,
為參數),以原點為極點,![]() 軸的非負半軸為極軸,且取相同的單位長度建立極坐標系,曲線
軸的非負半軸為極軸,且取相同的單位長度建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的普通方程及曲線
的普通方程及曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)設點![]() 的直角坐標為
的直角坐標為![]() ,直線
,直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】今年3月5日,國務院總理李克強作的政府工作報告中,提到要“懲戒學術不端,力戒學術不端,力戒浮躁之風”.教育部日前公布的《教育部2019年部門預算》中透露,2019年教育部擬抽檢博士學位論文約6000篇,預算為800萬元.國務院學位委員會、教育部2014年印發的《博士碩士學位論文抽檢辦法》通知中規定:每篇抽檢的學位論文送3位同行專家進行評議,3位專家中有2位以上(含2位)專家評議意見為“不合格”的學位論文,將認定為“存在問題學位論文”.有且只有1位專家評議意見為“不合格”的學位論文,將再送2位同行專家進得復評,2位復評專家中有1位以上(含1位)專家評議意見為“不合格”的學位論文,將認定為“存在問題學位論文”.設每篇學位論文被每位專家評議為“不合格”的概率均為![]() ,且各篇學位論文是否被評議為“不合格”相互獨立.
,且各篇學位論文是否被評議為“不合格”相互獨立.
(1)記一篇抽檢的學位論文被認定為“存在問題學位論文”的概率為![]() ,求
,求![]() ;
;
(2)若擬定每篇抽檢論文不需要復評的評審費用為900元,需要復評的評審費用為1500元;除評審費外,其它費用總計為100萬元.現以此方案實施,且抽檢論文為6000篇,問是否會超過預算?并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 是各項均為正數的等差數列,其中
是各項均為正數的等差數列,其中![]() ,且
,且![]() 成等比數列;數列
成等比數列;數列![]() 的前
的前![]() 項和為
項和為![]() ,滿足
,滿足![]() .
.
(1)求數列![]() 、
、![]() 的通項公式;
的通項公式;
(2)如果![]() ,設數列
,設數列![]() 的前
的前![]() 項和為
項和為![]() ,是否存在正整數
,是否存在正整數![]() ,使得
,使得![]() 成立,若存在,求出
成立,若存在,求出![]() 的最小值,若不存在,說明理由.
的最小值,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 是定義在
是定義在![]() 上的奇函數,當
上的奇函數,當![]() 時,
時,![]() .則下列結論正確的是( ).
.則下列結論正確的是( ).
A.當![]() 時,
時,![]()
B.函數![]() 有五個零點
有五個零點
C.若關于![]() 的方程
的方程![]() 有解,則實數
有解,則實數![]() 的取值范圍是
的取值范圍是![]()
D.對![]() ,
,![]() 恒成立
恒成立
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com