Question

【題目】某班級共有50名同學（男女各占一半），為弘揚傳統文化，班委組織了“古詩詞男女對抗賽”，將同學隨機分成25組，每組男女同學各一名，每名同學均回答同樣的五個不同問題，答對一題得一分，答錯或不答得零分，總分5分為滿分.最后25組同學得分如下表：

組別號	1	2	3	4	5	6	7	8	9	10	11	12	13
男同學得分	5	4	5	5	4	5	5	4	4	4	5	5	4
女同學得分	4	3	4	5	5	5	4	5	5	5	5	3	5
分差	1	1	1	0	-1	0	1	-1	-1	-1	0	2	-1
組別號	14	15	16	17	18	19	20	21	22	23	24	25
男同學得分	4	3	4	4	4	4	5	5	5	4	3	3
女同學得分	5	3	4	5	4	3	5	5	3	4	5	5
分差	-1	0	0	-1	0	1	0	0	2	0	-2	-2

（I）完成列聯表，并判斷是否有90%的把握認為“該次對抗賽是否得滿分”與“同學性別”有關；

（Ⅱ）某課題研究小組假設各組男女同學分差服從正態分布，首先根據前20組男女同學的分差確定和，然后根據后面5組同學的分差來檢驗模型，檢驗方法是：記后面5組男女同學分差與的差的絕對值分別為，若出現下列兩種情況之一，則不接受該模型，否則接受該模型.①存在；②記滿足的i的個數為k，在服從正態分布的總體（個體數無窮大）中任意取5個個體，其中落在區間內的個體數大于或等于k的概率為P，.

試問該課題研究小組是否會接受該模型.

	0.10	0.05	0.010
	2.706	3.841	6.635

參考公式和數據：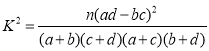

，；若，有，.

Answer 1

【答案】（I）列聯表見解析，沒有把握；（Ⅱ）第②種情況出現，所以該小組不會接受該模型.

【解析】

（I）由已知可得列聯表，再利用卡方公式計算即可；

（Ⅱ），由題知，而，故不存在 而滿足的i的個數為3，算出的概率為0.043，從服從總體（個體數無窮大）中任意取5個個體，其中值屬于的個體數為Y，則，再利用二項分布概率公式計算即可.

（I）由表可得

	男同學	女同學	總計
該次大賽得滿分	10	14	24
該次大賽未得滿分	15	11	26
總計	25	25	50

所以，

所以沒有90%的把握說“該次大賽是否得滿分”與“同學性別”有關；

（Ⅱ）由表格可得；

由題知，而，

故不存在 ，而滿足的i的個數為3，即

當

設從服從正態分布的總體（個體數無窮大）中任意取5個個體，其中值屬于

的個體數為Y，則，

所以，，

綜上，第②種情況出現，所以該小組不會接受該模型.

【點晴】

本題考查獨立性檢驗與正態分布的綜合應用，涉及到正態分布的概率計算問題，考查學生的數學運算能力，是一道有一定難度的題.