道路交通安全法中將飲酒后違法駕駛機動車的行為分成兩個檔次:“酒后駕車”和“醉酒駕車”,其檢測標準是駕駛人員血液中的酒精含量Q(簡稱血酒含量,單位是毫克/100毫升),當20≤Q<80時,為酒后駕車;當Q≥80時,為醉酒駕車.某市公安局交通管理部門在某路段的一次攔查行動中,依法檢查了200輛機動車駕駛員的血酒含量,其中查處酒后駕車的有6人,查處醉酒駕車的有2人,依據上述材料回答下列問題:
(1)分別寫出違法駕車發生的頻率和醉酒駕車占違法駕車總數的百分數.
(2)從違法駕車的8人中抽取2人,求取到醉酒駕車人數的分布列和期望,并指出所求期望的實際意義.
(3)飲酒后違法駕駛機動車極易發生交通事故,假設酒后駕車和醉酒駕車發生交通事故的概率分別是0.1和0.25,且每位駕駛員是否發生交通事故是相互獨立的.依此計算被查處的8名駕駛員中至少有一人發生交通事故的概率.(精確到0.01)并針對你的計算結果對駕駛員發出一句話的倡議.
解:(Ⅰ)由題意知檢查了200輛機動車駕駛員的血酒含量,
其中查處酒后駕車的有6人,查處醉酒駕車的有2人,
∴違法駕車發生的頻率=
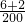
=

醉酒駕車占違法駕車總數的百分數為

=25%
(Ⅱ)解:設取到醉酒駕車的人數為隨機變量ξ,
則ξ可能取到的值有0,1,2
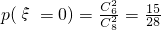
,
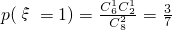
,

.

則分布列如下
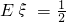
,實際意義:在抽取的兩人中平均含有0.5個醉酒駕車人員.
(Ⅲ)被查處的8名駕駛員中至少有一人發生交通事故的對立事件是沒有人發生交通事故,
由相互獨立事件同時發生的概率和對立事件的概率得到
p=1-0.9
6•0.75
2≈0.70
一句話倡議:答案開放,教師酌情給分.
分析:(Ⅰ)由題意知檢查了200輛機動車駕駛員的血酒含量,其中查處酒后駕車的有6人,查處醉酒駕車的有2人,違法駕車發生的頻率=
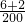
,醉酒駕車占違法駕車總數的百分數為

.
(2)由題意得到醉酒駕車的人數為隨機變量ξ,從違法駕車的8人中抽取2人,8人中最多有2人醉駕,得到ξ可能取到的值有0,1,2,根據古典概型概率公式得到結果.
(3)被查處的8名駕駛員中至少有一人發生交通事故的對立事件是沒有人發生交通事故,由相互獨立事件同時發生的概率和對立事件的概率得到要求的概率.
點評:考查運用概率知識解決實際問題的能力,相互獨立事件是指,兩事件發生的概率互不影響,注意應用相互獨立
事件同時發生的概率公式.

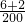 =
=
 =25%
=25%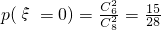 ,
,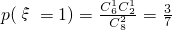 ,
, .
.
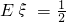 ,實際意義:在抽取的兩人中平均含有0.5個醉酒駕車人員.
,實際意義:在抽取的兩人中平均含有0.5個醉酒駕車人員.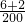 ,醉酒駕車占違法駕車總數的百分數為
,醉酒駕車占違法駕車總數的百分數為 .
.

 函數f(x)=Asin(ωx+φ)(其中
函數f(x)=Asin(ωx+φ)(其中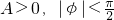 )的圖象如圖所示,為了得到g(x)=sin2x的圖象,則只需將f(x)的圖象
)的圖象如圖所示,為了得到g(x)=sin2x的圖象,則只需將f(x)的圖象 個長度單位
個長度單位 個長度單位
個長度單位 個長度單位
個長度單位 個長度單位
個長度單位 ,0),f(x)=log2(1-x),則f(2011)+f(2012)+f(2013)+f(2014)=
,0),f(x)=log2(1-x),則f(2011)+f(2012)+f(2013)+f(2014)=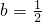 ,且k>0,問函數f(x)的圖象是不是軸對稱圖形?如果是,求出函數f(x)圖象的對稱軸;如果不是,請說明理由.
,且k>0,問函數f(x)的圖象是不是軸對稱圖形?如果是,求出函數f(x)圖象的對稱軸;如果不是,請說明理由.