
【題目】如圖,在三棱柱ABC![]() 中,側面
中,側面![]() 是矩形,∠BAC=90°,
是矩形,∠BAC=90°,![]() ⊥BC,
⊥BC,![]() =AC=2AB=4,且
=AC=2AB=4,且![]() ⊥
⊥![]() .
.

(1)求證:平面![]() ⊥平面
⊥平面![]() ;
;
(2)設D是![]() 的中點,判斷并證明在線段
的中點,判斷并證明在線段![]() 上是否存在點E,使得DE∥平面
上是否存在點E,使得DE∥平面![]() .若存在,求二面角E
.若存在,求二面角E![]() B的余弦值.
B的余弦值.
【答案】(1)見解析;(2)![]() .
.
【解析】分析:(1)易知![]() ⊥平面ABC,有
⊥平面ABC,有![]() ⊥AC,依次可證得
⊥AC,依次可證得![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() ,從而得證;
,從而得證;
(2)當E為![]() 的中點時,連接AE,
的中點時,連接AE,![]() ,DE,易證得平面EFD∥平面
,DE,易證得平面EFD∥平面![]() ,以 A為坐標原點,AB,AC,
,以 A為坐標原點,AB,AC,![]() 所在的直線分別為x軸、y軸、z軸建立如圖所示的空間直角坐標系,分別求面
所在的直線分別為x軸、y軸、z軸建立如圖所示的空間直角坐標系,分別求面![]() 和面
和面![]() 的法向量,由法向量的夾角可求二面角的余弦值.
的法向量,由法向量的夾角可求二面角的余弦值.
詳解:(1)在三棱柱ABC![]() 中,側面
中,側面![]() 是矩形,∴
是矩形,∴![]() ⊥AB,
⊥AB,
又![]() ⊥BC,AB∩BC=B,
⊥BC,AB∩BC=B,
∴![]() ⊥平面ABC,∴
⊥平面ABC,∴![]() ⊥AC.
⊥AC.
又![]() =AC,∴
=AC,∴![]() ⊥
⊥![]() .
.
又![]() ⊥
⊥![]() ,
,![]() ∩
∩![]() =
=![]() ,
,
∴![]() ⊥平面
⊥平面![]() ,
,
又![]()
![]() 平面
平面![]() ,∴平面
,∴平面![]() ⊥平面
⊥平面![]() .
.
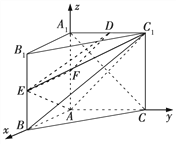
圖1
(2)解法一 當E為![]() 的中點時,連接AE,
的中點時,連接AE,![]() ,DE,如圖1,取
,DE,如圖1,取![]() 的中點F,連接EF,FD,
的中點F,連接EF,FD,
∵EF∥AB,DF∥![]() ,
,
又EF∩DF=F,AB∩![]() =A,
=A,
∴平面EFD∥平面![]() ,
,
則有DE∥平面![]() .
.
以 A為坐標原點,AB,AC,![]() 所在的直線分別為x軸、y軸、z軸建立如圖所示的空間直角坐標系,因為
所在的直線分別為x軸、y軸、z軸建立如圖所示的空間直角坐標系,因為![]() =AC=2AB=4,
=AC=2AB=4,
∴A(0,0,0),B(2,0,0),![]() (0,4,4),C(0,4,0),E(2,0,2),
(0,4,4),C(0,4,0),E(2,0,2),![]() (0,0,4),由(1)知,
(0,0,4),由(1)知,![]() =(0,4,4)是平面
=(0,4,4)是平面![]() 的一個法向量.
的一個法向量.
設n=(x,y,z)為平面![]() 的法向量,
的法向量,
∵![]() =(0,4,4),
=(0,4,4),![]() =(2,0,2),
=(2,0,2),
∴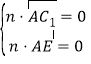
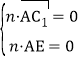 ,即
,即![]()
![]() ,
,
令z=1,則x=1,y=1,
∴n=(1,1,1)為平面![]() 的一個法向量.
的一個法向量.
設![]()
![]() 與n的夾角為θ,則cos θ=
與n的夾角為θ,則cos θ=![]() =
=![]()
![]() ,由圖知二面角E
,由圖知二面角E![]() B為銳角,∴二面角E
B為銳角,∴二面角E![]() B的余弦值為
B的余弦值為![]()
![]() .
.
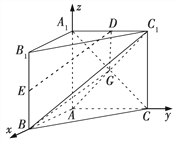
圖2
解法二 當E為![]() 的中點時,連接DE,如圖2,設
的中點時,連接DE,如圖2,設![]() 交
交![]() 于點G,連接BG,DG,∵BE
于點G,連接BG,DG,∵BE![]() DG,∴四邊形DEBG為平行四邊形,
DG,∴四邊形DEBG為平行四邊形,
則DE∥BG,又DE![]() 平面
平面![]() ,BG
,BG![]() 平面
平面![]() ,則DE∥平面
,則DE∥平面![]() .
.
求二面角E![]() B的余弦值同解法一.
B的余弦值同解法一.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】曲一中某研究性學習小組對學習數學的練習時間與進步率的關系進行研究,他們分別記錄了同班5個同學一周內的學習時間與周測成績進步率,得到如下資料.

(1)從5個同學中任選2個,記其進步率分別為![]() ,求事件“
,求事件“![]() 均不小于25”的概率;
均不小于25”的概率;
(2)若進步率![]() 與學習時間
與學習時間![]() 服從線性關系,求出
服從線性關系,求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(3)在這5個同學中任取3個,其中進步率超過25的有![]() 個同學,求
個同學,求![]() 的數學期望.
的數學期望.
參考公式:回歸直線方程是![]() ,其中
,其中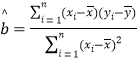
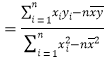
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】空氣質量指數(簡稱:![]() )是定量描述空氣質量狀況的無量綱指數,空氣質量按照
)是定量描述空氣質量狀況的無量綱指數,空氣質量按照![]() 大小分為六級:
大小分為六級:![]() 為優,
為優,![]() 為良,
為良,![]() 為輕度污染,
為輕度污染,![]() 為中度污染,
為中度污染,![]() 為重度污染,
為重度污染,![]() 為嚴重污染.下面記錄了北京市
為嚴重污染.下面記錄了北京市![]() 天的空氣質量指數,根據圖表,下列結論錯誤的是( )
天的空氣質量指數,根據圖表,下列結論錯誤的是( )

A. 在北京這![]() 天的空氣質量中,按平均數來考察,最后
天的空氣質量中,按平均數來考察,最后![]() 天的空氣質量優于最前面
天的空氣質量優于最前面![]() 天的空氣質量 B. 在北京這
天的空氣質量 B. 在北京這![]() 天的空氣質量中,有
天的空氣質量中,有![]() 天達到污染程度
天達到污染程度
C. 在北京這![]() 天的空氣質量中,12月29日空氣質量最好 D. 在北京這
天的空氣質量中,12月29日空氣質量最好 D. 在北京這![]() 天的空氣質量中,達到空氣質量優的天數有
天的空氣質量中,達到空氣質量優的天數有![]() 天
天
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直三棱柱ABC—A1B1C1中,BC=3,AB=4,AC=CC1=5,M,N分別是A1B,B1C1的中點.
(1)求證:MN//平面ACC1A1;
(2)求點N到平面MBC的距離.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設f(x)="xln" x–ax2+(2a–1)x,a![]() R.
R.
(Ⅰ)令g(x)=f'(x),求g(x)的單調區間;
(Ⅱ)已知f(x)在x=1處取得極大值.求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解中學生課余觀看熱門綜藝節目“爸爸去哪兒”是否與性別有關,某中學一研究性學習小組從該校學生中隨機抽取了![]() 人進行問卷調查.調查結果表明:女生中喜歡觀看該節目的占女生總人數的
人進行問卷調查.調查結果表明:女生中喜歡觀看該節目的占女生總人數的![]() ,男生喜歡看該節目的占男生總人數的
,男生喜歡看該節目的占男生總人數的![]() .隨后,該小組采用分層抽樣的方法從這
.隨后,該小組采用分層抽樣的方法從這![]() 份問卷中繼續抽取了
份問卷中繼續抽取了![]() 份進行重點分析,知道其中喜歡看該節目的有
份進行重點分析,知道其中喜歡看該節目的有![]() 人.
人.
(1) 現從重點分析的![]() 人中隨機抽取了
人中隨機抽取了![]() 人進行現場調查,求這兩人都喜歡看該節目的概率;
人進行現場調查,求這兩人都喜歡看該節目的概率;
(2) 若有![]() 的把握認為“愛看該節目與性別有關”,則參與調查的總人數
的把握認為“愛看該節目與性別有關”,則參與調查的總人數![]() 至少為多少?
至少為多少?
參考數據:
| 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() ,
,![]() 是函數
是函數![]() 的圖像上任意不同的兩點,依據圖像可知,線段
的圖像上任意不同的兩點,依據圖像可知,線段![]() 總是位于
總是位于![]() 兩點之間函數圖像的上方,因此有結論
兩點之間函數圖像的上方,因此有結論![]() 成立,運用類比的思想方法可知,若點
成立,運用類比的思想方法可知,若點![]() ,
,![]() 是函數
是函數![]() 的圖像上任意不同的兩點,則類似地有_________成立.
的圖像上任意不同的兩點,則類似地有_________成立.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學舉行電腦知識競賽,現將高一參賽學生的成績進行整理后分成五組繪制成如圖所示的頻率分布直方圖,已知圖中從左到右的第一、二、三、四、五小組的頻率分別是0.30,0.40,0.15,0.10,0.05.

求:(1)高一參賽學生的成績的眾數、中位數;
(2)高一參賽學生的平均成績.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com