【題目】若
是兩個相交平面，則在下列命題中，真命題的序號為 ．（寫出所有真命題的序號）
①若直線
，則在平面
內，一定不存在與直線
平行的直線．
②若直線
，則在平面
內，一定存在無數條直線與直線
垂直．
③若直線
，則在平面
內，不一定存在與直線
垂直的直線．
④若直線
，則在平面
內，一定存在與直線
垂直的直線．
期末金牌卷系列答案
輕松課堂標準練系列答案科目：高中數學 來源： 題型：
【題目】如圖，在底面是正方形的四棱錐P﹣ABCD中，PA⊥面ABCD，BD交AC于點E，F是PC中點，G為AC上一點．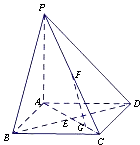 
（1）求證：BD⊥FG；
（2）確定點G在線段AC上的位置，使FG∥平面PBD，并說明理由；
（3）當二面角B﹣PC﹣D的大小為 
時，求PC與底面ABCD所成角的正切值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（本題滿分16分）數列
， 
， 
滿足： 
， 
， 
．
（1）若數列
是等差數列，求證：數列
是等差數列；
（2）若數列
， 
都是等差數列，求證：數列
從第二項起為等差數列；
（3）若數列
是等差數列，試判斷當
時，數列
是否成等差數列？證明你的結論．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=ln（x+ 
﹣2）（a＞0） （Ⅰ）當1＜a＜4時，函數f（x）在[2，4]上的最小值為ln 
，求a；
（Ⅱ）若存在x0∈（2，+∞），使得f（x0）＜0，求a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖是我國南宋時期的數學家秦九韶提出的一種多項式f（x）=anxn+an﹣1xn﹣1+…+a1x+a0的求值問題的算法．現按照這個程序執行函數f （x）=3x4﹣2x3﹣6x﹣17的計算，若輸入的值x0=2，則輸出的v的值是（ ） 
A.0
B.2
C.3
D.﹣3
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在半徑為 
，圓心角為60°的扇形的弧上任取一點P，作扇形的內接矩形PNMQ，使點Q在OA上，點N，M在OB上，設矩形PNMQ的面積為y，∠POB=θ．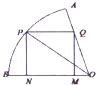 
（1）將y表示成θ的函數關系式，并寫出定義域；
（2）求矩形PNMQ的面積取得最大值時 
的值；
（3）求矩形PNMQ的面積y≥ 
的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=mex﹣x﹣1（其中e為自然對數的底數，），若f（x）=0有兩根x1 ， x2且x1＜x2 ， 則函數y=（e 
﹣e 
）（ 
﹣m）的值域為 ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】從1開始的自然數按如圖所示的規則排列，現有一個三角形框架在圖中上下或左右移動，使每次恰有九個數在此三角形內，則這九個數的和可以為（ ）
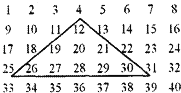
A.2097 B.2112 C.2012 D.2090
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
