
【題目】為了了解居民的家庭收人情況,某社區組織工作人員從該社區的居民中隨機抽取了![]() 戶家庭進行問卷調查.經調查發現,這些家庭的月收人在
戶家庭進行問卷調查.經調查發現,這些家庭的月收人在![]() 元到
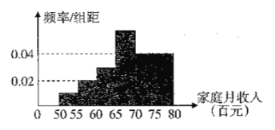
元到![]() 元之間,根據統計數據作出如圖所示的頻率分布直方圖.已知圖中從左至右第一 、二、四小組的頻率之比為
元之間,根據統計數據作出如圖所示的頻率分布直方圖.已知圖中從左至右第一 、二、四小組的頻率之比為![]() ,且第四小組的頻數為
,且第四小組的頻數為![]() .
.
(1)求![]() ;
;
(2)求這![]() 戶家庭月收人的眾數與中位數(結果精確到
戶家庭月收人的眾數與中位數(結果精確到![]() );
);
(3)這![]() 戶家庭月收入在第一、二、三小組的家庭中,用分層抽樣的方法任意抽取
戶家庭月收入在第一、二、三小組的家庭中,用分層抽樣的方法任意抽取![]() 戶家庭,并從這
戶家庭,并從這![]() 戶家庭中隨機抽取
戶家庭中隨機抽取![]() 戶家庭進行慰問,求這
戶家庭進行慰問,求這![]() 戶家庭月收入都不超過
戶家庭月收入都不超過![]() 元的概率.
元的概率.
【答案】(1)![]() (2)眾數是67.5,中位數是66.3 (3)
(2)眾數是67.5,中位數是66.3 (3)![]()
【解析】
(1)根據從左至右第一 、二、四小組的頻率之比為![]() ,求出第四小組的頻率,再由頻率
,求出第四小組的頻率,再由頻率![]() 即可求解.
即可求解.
(2)由頻率分布直方圖第四組小矩形底邊中點的橫坐標為眾數;中位數等于各個小矩形面積與其小矩形底邊中點橫坐標之積的和.
(3)根據分層抽樣得出第一、二、三小組應分別抽取![]() ,分別記記為
,分別記記為![]()
依次列出基本事件個數,由古典概型的概率求法公式即可求解.
解:(Ⅰ)設從左至右第一、三、四小組的頻率分別為![]() ,則由題意可知:
,則由題意可知:
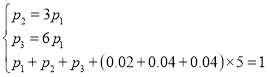 ,解得
,解得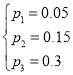
從而![]()
(2)由于第四小組頻率最大,故這 ![]() 戶家庭月收入的眾數為
戶家庭月收入的眾數為![]()
由于前四小組的頻率之和為:![]()
故這![]() 戶家庭月收入的中位數應落在第四小組,設中位數為
戶家庭月收入的中位數應落在第四小組,設中位數為 ![]()
則![]() ,解得
,解得![]()
(3)因為家庭月收入在第一、二、三小組的家庭分別有![]() 戶,按照分層抽樣的方法易知分別抽取
戶,按照分層抽樣的方法易知分別抽取![]() ,第一組記為
,第一組記為![]() ,第二組
,第二組![]() ,第三組為
,第三組為![]() ,
,
從中隨機抽取2 戶家庭的方法共有![]()
![]() 共
共![]() 種;
種;
其中這![]() 戶家庭月收入都不超過
戶家庭月收入都不超過![]() 元的有
元的有
![]()
![]() 共
共![]() 種;
種;
所以這![]() 戶家庭月收入都不超過
戶家庭月收入都不超過![]() 元的概率為
元的概率為![]()


科目:高中數學 來源: 題型:
【題目】用一個長為![]() ,寬為
,寬為![]() 的矩形鐵皮(如圖1)制作成一個直角圓形彎管(如圖3):先在矩形的中間畫一條曲線,并沿曲線剪開,將所得的兩部分分別卷成體積相等的斜截圓柱狀(如圖2),然后將其中一個適當翻轉拼接成直角圓形彎管(如圖3)(不計拼接損耗部分),并使得直角圓形彎管的體積最大;
的矩形鐵皮(如圖1)制作成一個直角圓形彎管(如圖3):先在矩形的中間畫一條曲線,并沿曲線剪開,將所得的兩部分分別卷成體積相等的斜截圓柱狀(如圖2),然后將其中一個適當翻轉拼接成直角圓形彎管(如圖3)(不計拼接損耗部分),并使得直角圓形彎管的體積最大;
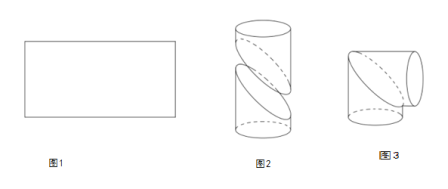
(1)求直角圓形彎管(圖3)的體積;
(2)求斜截面橢圓的焦距;
(3)在相應的圖1中建立適當的坐標系,使所畫的曲線的方程為![]() ,求出方程并畫出大致圖像;
,求出方程并畫出大致圖像;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的一個焦點為
的一個焦點為![]() ,離心率為
,離心率為![]() .
.
(1)求![]() 的標準方程;
的標準方程;
(2)若動點![]() 為
為![]() 外一點,且
外一點,且![]() 到
到![]() 的兩條切線相互垂直,求
的兩條切線相互垂直,求![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(3)設![]() 的另一個焦點為
的另一個焦點為![]() ,過
,過![]() 上一點
上一點![]() 的切線與(2)所求軌跡
的切線與(2)所求軌跡![]() 交于點
交于點![]() ,
,![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】實數a,b滿足ab>0且a≠b,由a、b、![]() 、
、![]() 按一定順序構成的數列( )
按一定順序構成的數列( )
A. 可能是等差數列,也可能是等比數列
B. 可能是等差數列,但不可能是等比數列
C. 不可能是等差數列,但可能是等比數列
D. 不可能是等差數列,也不可能是等比數列
查看答案和解析>>
科目:高中數學 來源: 題型:
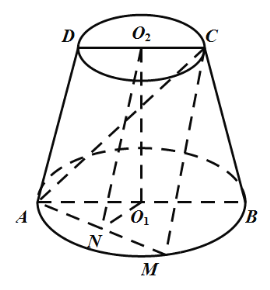
【題目】如圖,在圓臺![]() 中,平面
中,平面![]() 過上下底面的圓心
過上下底面的圓心![]() ,
,![]() ,點M在
,點M在![]() 上,N為
上,N為![]() 的中點,
的中點,![]() .
.
(1)求證:平面![]() 平面
平面![]() ;
;
(2)當![]() 時,
時,![]() 與底面
與底面![]() 所成角的正弦值為
所成角的正弦值為![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
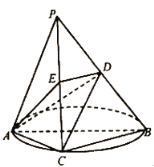
【題目】如圖,![]() 是一個三棱錐,
是一個三棱錐,![]() 是圓的直徑,
是圓的直徑,![]() 是圓上的點,
是圓上的點,![]() 垂直圓所在的平面,
垂直圓所在的平面,![]() ,
,![]() 分別是棱
分別是棱![]() ,
,![]() 的中點.
的中點.
(1)求證:![]() 平面
平面![]() ;
;
(2)若二面角![]() 是
是![]() ,
,![]() ,求
,求![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了鼓勵職員工作熱情,某公司對每位職員一年來的工作業績按月進行考評打分;年終按照職員的月平均值評選公司最佳職員并給予相應獎勵.已知職員![]() 一年來的工作業績分數的莖葉圖如圖所示:
一年來的工作業績分數的莖葉圖如圖所示:
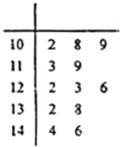
(1)根據職員![]() 的業績莖葉圖求出他這一年的工作業績的中位數和平均數;
的業績莖葉圖求出他這一年的工作業績的中位數和平均數;
(2)由于職員![]() 的業績高,被公司評為年度最佳職員,在公司年會上通過抽獎形式領取獎金.公司準備了六張卡片,其中一張卡片上標注獎金為6千元,兩張卡片的獎金為4千元,另外三張的獎金為2千元.規則是:獲獎職員
的業績高,被公司評為年度最佳職員,在公司年會上通過抽獎形式領取獎金.公司準備了六張卡片,其中一張卡片上標注獎金為6千元,兩張卡片的獎金為4千元,另外三張的獎金為2千元.規則是:獲獎職員![]() 需要從六張卡片中隨機抽出兩張,這兩張卡片上的金額數之和作為獎金數.求職員
需要從六張卡片中隨機抽出兩張,這兩張卡片上的金額數之和作為獎金數.求職員![]() 獲得獎金6千元的概率;并說明獲得獎金6千元和8千元哪個可能性較大?
獲得獎金6千元的概率;并說明獲得獎金6千元和8千元哪個可能性較大?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com