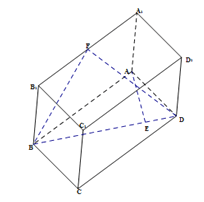
【題目】如圖，長方體
中， 
， 
，點
， 
， 
分別為
， 
， 
的中點，過點
的平面
與平面
平行，且與長方體的面相交，交線圍成一個幾何圖形.
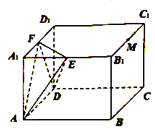
（1）在圖中畫出這個幾何圖形（說明畫法，不需要說明理由）；
（2）求二面角
的余弦值.
【答案】（1）見解析；（2）
.
【解析】試題分析：（1）利用平行關系作圖；（2）建立空間直角坐標系，求出兩個法向量， 
， 
，求出二面角。
試題解析：
（1）取
的中點
，連接
， 
， 
， 
，則交線圍成的幾何圖形
如圖：
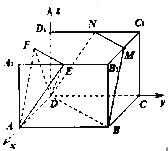
（2）因為點
， 
分別為
， 
的中點， 
，
所以
， 
以
為坐標原點， 
的方向為
軸的正方向，建立如圖所示空間直角坐標系
，則
， 
， 
，
， 
.
設
是平面
的法向量，則
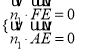，即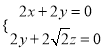
所以可取
.
同理可求平面
的一個法向量為
因為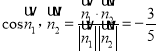
所以二面角
的余弦值為
試題分析：本題考查立體幾何的二面角求解。一般的，在容易建系的立體幾何問題中，采取空間直角坐標系解題比較方便，可以避免找角或其他技巧性方法，將幾何問題轉化為代數計算，只需掌握解題套路，即可解決問題。
中考利劍中考試卷匯編系列答案
教育世家狀元卷系列答案
黃岡課堂作業本系列答案科目：高中數學 來源： 題型：
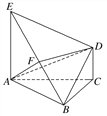
【題目】如圖所示，底面ABC為正三角形，EA⊥平面ABC，DC⊥平面ABC，EA＝AB＝2DC＝2a，設F為EB的中點．
(1)求證：DF∥平面ABC；
(2)求直線AD與平面AEB所成角的正弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】橢圓C： 
的左、右頂點分別為A1、A2，點P在C上且直線PA2的斜率的取值范圍是[－2，－1]，那么直線PA1斜率的取值范圍是________.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f(x)＝xlnx和g(x)＝m(x2－1)(m∈R)．
(1)m＝1時，求方程f(x)＝g(x)的實根；
(2)若對任意的x∈(1，＋∞)，函數y＝g(x)的圖象總在函數y＝f(x)圖象的上方，求m的取值范圍；
(3)求證： 
＋
＋…＋
>ln(2n＋1) (n∈N*)．
查看答案和解析>>
科目：高中數學 來源： 題型：
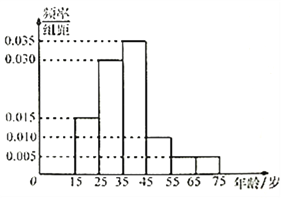
【題目】2017年5月14日,第一屆“一帶一路”國際高峰論壇在北京舉行,為了解不同年齡的人對“一帶一路”關注程度,某機構隨機抽取了年齡在
歲之間的100人進行調查,并按年齡繪制成頻率分布直方圖,如圖所示,其分組區間為: 
, 
,
,
,
,
.把年齡落在區間
和
內的人分別稱為“青少年”和“中老年”.
(1)根據頻率分布直方圖求樣本的中位數(保留兩位小數)和眾數
(2)根據已知條件完成下面的2×2列聯表,并判斷能否有99%的把握認為關注“帶一路”是否和年齡段有關?
關注 | 不關注 | 合計 | |
青少年 | 15 | ||
中老年 | |||
合計 | 50 | 50 | 100 |
附:參考公式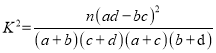
，其中
臨界值表：
| 0.05 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，已知長方體
，直線
與平面
所成角為
垂直
于點
為
的中點.
（1）求直線
與平面
所成角的正弦值；
（2）線段
上是否存在點
，使得二面角
的余弦值為
？若存在，確定
點位置；若不存在，說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
