
已知函數(shù)f(x)=x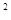 +2ax+2, x
+2ax+2, x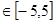 .
.
(1)當(dāng)a=-1時,求函數(shù)的最大值和最小值;
(2) 若y=f(x)在區(qū)間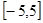 上是單調(diào) 函數(shù),求實(shí)數(shù) a的取值范圍.
上是單調(diào) 函數(shù),求實(shí)數(shù) a的取值范圍.
 云南師大附小一線名師提優(yōu)作業(yè)系列答案
云南師大附小一線名師提優(yōu)作業(yè)系列答案 沖刺100分單元優(yōu)化練考卷系列答案
沖刺100分單元優(yōu)化練考卷系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分12分)已知y= 是二次函數(shù),且f(0)=8及f(x+1)-f(x)=-2x+1
是二次函數(shù),且f(0)=8及f(x+1)-f(x)=-2x+1
(1)求 的解析式;
的解析式;
(2)求函數(shù) 的單調(diào)遞減區(qū)間及值域..
的單調(diào)遞減區(qū)間及值域..
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題共12分)
已知函數(shù)f(x)=2x-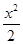 -aln(x+1),a∈R.(1)若a=-4,求函數(shù)f(x)的單調(diào)區(qū)間;
-aln(x+1),a∈R.(1)若a=-4,求函數(shù)f(x)的單調(diào)區(qū)間;
(2)求y=f(x)的極值點(diǎn)(即函數(shù)取到極值時點(diǎn)的橫坐標(biāo)).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本大題13分)設(shè)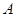 、
、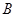 為函數(shù)
為函數(shù)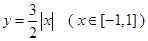 圖象上不同的兩個點(diǎn),
圖象上不同的兩個點(diǎn),
且 AB∥ 軸,又有定點(diǎn)
軸,又有定點(diǎn)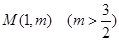 ,已知
,已知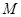 是線段
是線段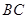 的中點(diǎn).
的中點(diǎn).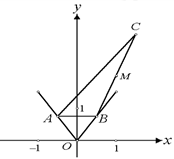
⑴ 設(shè)點(diǎn) 的橫坐標(biāo)為
的橫坐標(biāo)為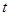 ,寫出
,寫出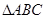 的面積
的面積 關(guān)于
關(guān)于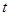 的函數(shù)
的函數(shù)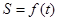 的表達(dá)式;
的表達(dá)式;
⑵ 求函數(shù)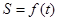 的最大值,并求此時點(diǎn)
的最大值,并求此時點(diǎn)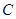 的坐標(biāo)。
的坐標(biāo)。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù)
⑴若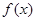 的定義域和值域均是
的定義域和值域均是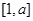 ,求實(shí)數(shù)
,求實(shí)數(shù)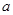 的值;
的值;
⑵若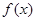 在
在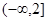 上是減函數(shù),且對任意的
上是減函數(shù),且對任意的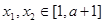 ,總有
,總有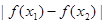 ≤
≤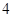 ,求實(shí)數(shù)
,求實(shí)數(shù)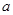 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本題滿分13分)
已知函數(shù) 滿足
滿足 ;
;
(1)若方程 有唯一解,求
有唯一解,求 的值;
的值;
(2)若函數(shù) 在區(qū)間
在區(qū)間 上不是單調(diào)函數(shù),求實(shí)數(shù)
上不是單調(diào)函數(shù),求實(shí)數(shù) 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(15分)已知:二次函數(shù)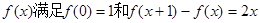 .
.
(1)求 的解析式;
的解析式;
(2)若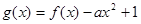 有一個正的零點(diǎn),求實(shí)數(shù)
有一個正的零點(diǎn),求實(shí)數(shù) 的取值范圍。
的取值范圍。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分12分)
設(shè)函數(shù)f(x)=x2-2x+2,x∈[t,t+1](t∈R)的最小值為g(t),求g(t)的表達(dá)式.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知一家公司生產(chǎn)某種品牌服裝的年固定成本為10萬元,每生產(chǎn)1千件需另投入2.7萬元.設(shè)該公司一年內(nèi)共生產(chǎn)該品牌服裝x千件并全部銷售完,每千件的銷售收入為R(x)萬元,且R(x)=
(1)寫出年利潤W(萬元)關(guān)于年產(chǎn)量x(千件)的函數(shù)解析式;
(2)年產(chǎn)量為多少千件時,該公司在這一品牌服裝的生產(chǎn)中所獲得利潤最大?(注:年利潤=年銷售收入-年總成本)
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com