
【題目】某人有兩盒火柴,每盒都有![]() 根火柴,每次用火柴時他在兩盒中任取一盒并從中抽出一根,求他發現用完一盒時另一盒還有
根火柴,每次用火柴時他在兩盒中任取一盒并從中抽出一根,求他發現用完一盒時另一盒還有![]() 根(
根(![]() )的概率_____.
)的概率_____.
科目:高中數學 來源: 題型:
【題目】![]() 是定義在
是定義在![]() 上且滿足如下條件的函數
上且滿足如下條件的函數![]() 組成的集合:①對任意的
組成的集合:①對任意的![]() ,都有
,都有![]() ②存在常數
②存在常數![]() 使得對任意的
使得對任意的![]() ,都有
,都有![]() .
.
(1)設![]() 問
問![]() 是否屬于
是否屬于![]() ?說明理由;
?說明理由;
(2)若![]() 如果存在
如果存在![]() 使得
使得![]() 證明:這樣的
證明:這樣的![]() 是唯一的;
是唯一的;
(3)設![]() 且
且![]() 試求
試求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在一個給定的正![]() 邊形的頂點中隨機地選取三個不同的頂點,任何一種選法的可能性是相等的,則正多邊形的中心位于所選三個點構成的三角形內部的概率為______.
邊形的頂點中隨機地選取三個不同的頂點,任何一種選法的可能性是相等的,則正多邊形的中心位于所選三個點構成的三角形內部的概率為______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,若同時滿足以下條件:
,若同時滿足以下條件:
①![]() 在D上單調遞減或單調遞增;
在D上單調遞減或單調遞增;
②存在區間![]() ,使
,使![]() 在
在![]() 上的值域是
上的值域是![]() ,那么稱
,那么稱![]() 為閉函數.
為閉函數.
(1)求閉函數![]() 符合條件②的區間
符合條件②的區間![]() ;
;
(2)判斷函數![]() 是不是閉函數?若是請找出區間
是不是閉函數?若是請找出區間![]() ;若不是請說明理由;
;若不是請說明理由;
(3)若![]() 是閉函數,求實數
是閉函數,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 在區間
在區間![]() 上的最大值為4,最小值為1,記為
上的最大值為4,最小值為1,記為![]() .
.
(1)求實數![]() ,
,![]() 的值;
的值;
(2)若不等式![]() 成立,求實數
成立,求實數![]() 的取值范圍;
的取值范圍;
(3)對于任意滿足![]() 的自變量
的自變量![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,如果存在一個常數
,如果存在一個常數![]() ,使得定義在區間
,使得定義在區間![]() 上的一個函數
上的一個函數![]() ,
,![]() 恒成立,則稱函數
恒成立,則稱函數![]() 為區間
為區間![]() 上的有界變差函數,試判斷函數
上的有界變差函數,試判斷函數![]() 是否是區間
是否是區間![]() 上的有界變差函數,若是,求出
上的有界變差函數,若是,求出![]() 的最小值;若不是,請說明理由.
的最小值;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 是
是![]() 上的偶函數,對于
上的偶函數,對于![]() 都有
都有![]() 成立,且
成立,且![]() ,當
,當![]() ,
,![]() ,且
,且![]() 時,都有
時,都有![]() .則給出下列命題:①
.則給出下列命題:①![]() ;②
;②![]() 為函數
為函數![]() 圖象的一條對稱軸;③函數
圖象的一條對稱軸;③函數![]() 在
在![]() 上為減函數;④方程
上為減函數;④方程![]() 在
在![]() 上有4個根;其中正確的命題個數為( )
上有4個根;其中正確的命題個數為( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() ,
,![]() 為其前
為其前![]() 項的和,滿足
項的和,滿足![]() .
.
(1)求數列![]() 的通項公式;
的通項公式;
(2)設數列![]() 的前
的前![]() 項和為
項和為![]() ,數列
,數列![]() 的前
的前![]() 項和為
項和為![]() ,求證:當
,求證:當![]() ,
,![]() 時
時![]() ;
;
(3)已知當![]() ,且
,且![]() 時有
時有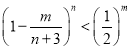 ,其中
,其中![]() ,求滿足
,求滿足![]() 的所有
的所有![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com