
【題目】設![]() ,函數
,函數![]() .
.
(1)當![]() 時,求
時,求![]() 在
在![]() 上的單調區間;
上的單調區間;
(2)設函數![]() ,當
,當![]() 有兩個極值點
有兩個極值點![]() 時,總有
時,總有![]() ,求實數
,求實數![]() 的值.
的值.
【答案】(1)增區間是 ![]() ,減區間是
,減區間是![]() ;(2)
;(2)![]() .
.
【解析】試題分析:(1)當![]() 時,求得
時,求得![]() ,求導
,求導![]() ,令
,令![]() ,則
,則![]() 在
在![]() 是減函數,從而
是減函數,從而![]() 在
在![]() 上是減函數,進而得出
上是減函數,進而得出![]() 在
在![]() 上的極大值
上的極大值![]() ,即可得到最大值;(2)由題意得可知
,即可得到最大值;(2)由題意得可知![]() ,則
,則![]() ,從而得不等式可化為
,從而得不等式可化為![]() ,對任意的
,對任意的![]() 恒成立.通過討論①當
恒成立.通過討論①當![]() 時,②當
時,②當![]() 時,③
時,③![]() 時的情況,即可得出結論.
時的情況,即可得出結論.
試題解析:(1)當![]() 時,
時,![]()
則![]() ,令
,令![]() ,則
,則![]()
顯然![]() 在區間
在區間![]() 內是減函數,又
內是減函數,又![]() ,在區間
,在區間![]() 內,總有
內,總有![]()
![]() 在區間
在區間![]() 內是減函數,又
內是減函數,又![]() 當
當![]() 時,
時,![]() ,
,
![]() ,此時
,此時![]() 單調遞增;
單調遞增;
當![]() 時,
時,![]()
![]() ,此時
,此時![]() 單調遞減;
單調遞減;
![]() 在區間
在區間![]() 內的極大值也即最大值是
內的極大值也即最大值是![]()
(2)由題意,知![]() ,則
,則![]()
根據題意,方程![]() 有兩個不同的實根
有兩個不同的實根![]()
![]() ,即
,即![]() ,且
,且![]()
![]() ,由
,由![]()
其中![]() ,得
,得![]()
![]()
所以上式化為![]()
又![]() ,所以不等式可化為
,所以不等式可化為![]() ,對任意的
,對任意的![]() 恒成立.
恒成立.
①當![]() ,
,![]() 不等式恒成立,
不等式恒成立,![]() ;
;
②當![]() 時,
時,![]() 恒成立,
恒成立,![]()
令函數![]()
顯然![]() 是
是![]() 內的減函數,當
內的減函數,當![]() ,
,![]()
③![]() 時,
時,![]() 恒成立,即
恒成立,即![]()
由②,當![]() ,
,![]() ,即
,即![]()


 暑假作業暑假快樂練西安出版社系列答案
暑假作業暑假快樂練西安出版社系列答案科目:高中數學 來源: 題型:
【題目】如圖,三棱柱ABC﹣A1B1C1中,AC=AA1=2,AB=BC=2 ![]() ,∠AA1C1=60°,平面ABC1⊥平面AA1C1C,AC1與A1C相交于點D.
,∠AA1C1=60°,平面ABC1⊥平面AA1C1C,AC1與A1C相交于點D. 
(1)求證:BC1⊥平面AA1C1C;
(2)求二面角C1﹣AB﹣C的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某超市為了解端午節期間粽子的銷售量,對其所在銷售范圍內的1000名消費者在端午節期間的粽子購買量(單位:g)進行了問卷調查,得到如圖所示的頻率分布直方圖.

(Ⅰ)求頻率分布直方圖中a的值;
(Ⅱ)求這1000名消費者的棕子購買量在600g~1400g的人數;
(Ⅲ)求這1000名消費者的人均粽子購買量(頻率分布直方圖中同一組的數據用該組區間的中點值作代表).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,三條直線型公路![]() ,
,![]() ,
,![]() 在點
在點![]() 處交匯,其中
處交匯,其中![]() 與
與![]() 、
、![]() 與
與![]() 的夾角都為
的夾角都為![]() ,在公路
,在公路![]() 上取一點
上取一點![]() ,且
,且![]() km,過
km,過![]() 鋪設一直線型的管道
鋪設一直線型的管道![]() ,其中點
,其中點![]() 在
在![]() 上,點
上,點![]() 在
在![]() 上(
上(![]() ,
,![]() 足夠長),設
足夠長),設![]() km,
km,![]() km.
km.
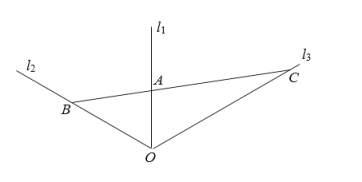
(1)求出![]() ,
,![]() 的關系式;
的關系式;
(2)試確定![]() ,
,![]() 的位置,使得公路
的位置,使得公路![]() 段與
段與![]() 段的長度之和最小.
段的長度之和最小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某超市計劃按月訂購一種酸奶,每天進貨量相同,進貨成本每瓶4元,售價每瓶6元,未售出的酸奶降價處理,以每瓶2元的價格當天全部處理完.根據往年銷售經驗,每天需求量與當天最高氣溫(單位:![]() )有關.如果最高氣溫不低于25,需求量為500瓶;如果最高氣溫位于區間
)有關.如果最高氣溫不低于25,需求量為500瓶;如果最高氣溫位于區間![]() ,需求量為300瓶;如果最高氣溫低于20,需求量為200瓶.為了確定六月份的訂購計劃,統計了前三年六月份各天的最高氣溫數據,得下面的頻數分布表:
,需求量為300瓶;如果最高氣溫低于20,需求量為200瓶.為了確定六月份的訂購計劃,統計了前三年六月份各天的最高氣溫數據,得下面的頻數分布表:
![]()
以最高氣溫位于各區間的頻率估計最高氣溫位于該區間的概率.
(1)求六月份這種酸奶一天的需求量![]() (單位:瓶)的分布列;
(單位:瓶)的分布列;
(2)設六月份一天銷售這種酸奶的利潤為![]() (單位:元),當六月份這種酸奶一天的進貨量
(單位:元),當六月份這種酸奶一天的進貨量![]() (單位:瓶)為多少時,
(單位:瓶)為多少時,![]() 的數學期望達到最大值?
的數學期望達到最大值?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有人用三段論進行推理:“函數![]() 的導函數
的導函數![]() 的零點即為函數
的零點即為函數![]() 的極值點,函數
的極值點,函數![]() 的導函數的零點為
的導函數的零點為![]() ,所以
,所以![]() 是函數
是函數![]() 的極值點 ”,上面的推理錯誤的是( )
的極值點 ”,上面的推理錯誤的是( )
A. 大前提 B. 小前提 C. 推理形式 D. 以上都是
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x3+ax2+bx+c,x∈[-2,2]表示過原點的曲線,且在x=±1處的切線的傾斜角均為![]() π,有以下命題:
π,有以下命題:
①f(x)的解析式為f(x)=x3-4x,x∈[-2,2].
②f(x)的極值點有且只有一個.
③f(x)的最大值與最小值之和等于零.
其中正確命題的序號為________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》是中國古代第一部數學專著,成于公元一世紀左右,系統總結了戰國、秦、漢時期的數學成就.其中《方田》一章中記載了計算弧田(弧田就是由圓弧和其所對弦所圍成弓形)的面積所用的經驗公式:弧田面積=![]() (弦×矢+矢×矢),公式中“弦”指圓弧所對弦長,“矢”等于半徑長與圓心到弦的距離之差.按照上述經驗公式計算所得弧田面積與其實際面積之間存在誤差.現有圓心角為
(弦×矢+矢×矢),公式中“弦”指圓弧所對弦長,“矢”等于半徑長與圓心到弦的距離之差.按照上述經驗公式計算所得弧田面積與其實際面積之間存在誤差.現有圓心角為![]() ,弦長為
,弦長為![]() 的弧田.其實際面積與按照上述經驗公式計算出弧田的面積之間的誤差為( )平方米.(其中
的弧田.其實際面積與按照上述經驗公式計算出弧田的面積之間的誤差為( )平方米.(其中![]() ,
,![]() )
)
A. 15 B. 16 C. 17 D. 18
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com