
【題目】已知![]() ,
, ![]() 分別是橢圓
分別是橢圓![]() :
: ![]() (
(![]() )的左、右焦點,離心率為
)的左、右焦點,離心率為![]() ,
, ![]() ,
, ![]() 分別是橢圓的上、下頂點,
分別是橢圓的上、下頂點, ![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)過![]() 作直線
作直線![]() 與
與![]() 交于
交于![]() ,
, ![]() 兩點,求三角形
兩點,求三角形![]() 面積的最大值(
面積的最大值(![]() 是坐標原點).
是坐標原點).
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】試題分析:(1)根據(jù)離心率為![]() ,
, ![]() ,列出關于
,列出關于![]() 、
、![]() 、
、![]() 的方程組,結合性質
的方程組,結合性質![]() ,求出
,求出![]() 、
、![]() 、
、![]() ,即可得橢圓
,即可得橢圓![]() 的方程;(2)直線
的方程;(2)直線![]() 斜率存在,設其方程為
斜率存在,設其方程為![]() .,直線方程與橢圓方程聯(lián)立,根據(jù)韋達定理,弦長公式、點到直線距離公式及三角形面積公式將角形
.,直線方程與橢圓方程聯(lián)立,根據(jù)韋達定理,弦長公式、點到直線距離公式及三角形面積公式將角形![]() 面積用
面積用![]() 表示,利用基本不等式 即可得結果.
表示,利用基本不等式 即可得結果.
試題解析:(1)由題知, ![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,∴
,∴![]() ,①
,①
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,②
,②
①②聯(lián)立解得![]() ,
, ![]() ,∴橢圓
,∴橢圓![]() 的方程為
的方程為![]() .
.
(2)設![]() ,
, ![]() ,顯然直線
,顯然直線![]() 斜率存在,設其方程為
斜率存在,設其方程為![]() ,
,
代入![]() ,整理得
,整理得![]() ,
,
則![]() ,即
,即![]() ,
, ![]() ,
, ![]() ,
,
![]()
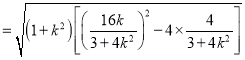
 ,
,
所以![]() 到
到![]() 的距離
的距離![]() ,
,
所以三角形![]() 面積
面積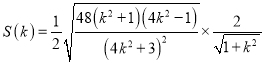
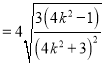 ,
,
設![]() ,所以
,所以 ,
,
當且僅當![]() ,即
,即![]() ,即
,即![]() ,即
,即![]() 時取等號,
時取等號,
所以![]() 面積的最大值為
面積的最大值為![]() .
.
【方法點晴】本題主要考查待定系數(shù)法求橢圓方程及圓錐曲線求最值,屬于難題.解決圓錐曲線中的最值問題一般有兩種方法:一是幾何意義,特別是用圓錐曲線的定義和平面幾何的有關結論來解決,非常巧妙;二是將圓錐曲線中最值問題轉化為函數(shù)問題,然后根據(jù)函數(shù)的特征選用參數(shù)法、配方法、判別式法、三角函數(shù)有界法、函數(shù)單調性法以及均值不等式法,本題(2)就是用的這種思路,利用均值不等式法求三角形最值的.


科目:高中數(shù)學 來源: 題型:
【題目】對某電子元件進行壽命追蹤調查,情況如下.
壽命(h) | 100~200 | 200~300 | 300~400 | 400~500 | 500~600 |
個 數(shù) | 20 | 30 | 80 | 40 | 30 |
(1)列出頻率分布表;
(2)畫出頻率分布直方圖;
(3)估計元件壽命在100~400h以內的在總體中占的比例.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】下列各函數(shù)在其定義域中,既是奇函數(shù),又是增函數(shù)的是( )
A.y=x+1
B.y=﹣x3
C.y=﹣ ![]()
D.y=x|x|
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)f(x)= ![]() .
.
(1)判斷并用定義證明函數(shù)的奇偶性;
(2)判斷并用定義證明函數(shù)在(﹣∞,0)上的單調性.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓 ![]() 的左、右焦點分別為F1、F2 , 短軸兩個端點為A、B,且四邊形F1AF2B是邊長為2的正方形.
的左、右焦點分別為F1、F2 , 短軸兩個端點為A、B,且四邊形F1AF2B是邊長為2的正方形. 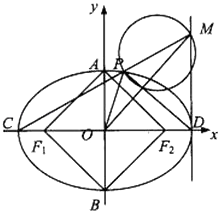
(1)求橢圓的方程;
(2)若C、D分別是橢圓長的左、右端點,動點M滿足MD⊥CD,連接CM,交橢圓于點P.證明: ![]() 為定值.
為定值.
(3)在(2)的條件下,試問x軸上是否存異于點C的定點Q,使得以MP為直徑的圓恒過直線DP、MQ的交點,若存在,求出點Q的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某廠家舉行大型的促銷活動,經測算某產品當促銷費用為![]() 萬元時,銷售量
萬元時,銷售量![]() 萬件滿足
萬件滿足![]() (其中
(其中![]() ,
, ![]() 為正常數(shù)),現(xiàn)假定生產量與銷售量相等,已知生產該產品
為正常數(shù)),現(xiàn)假定生產量與銷售量相等,已知生產該產品![]() 萬件還需投入成本
萬件還需投入成本![]() 萬元(不含促銷費用),產品的銷售價格定為
萬元(不含促銷費用),產品的銷售價格定為![]() 萬元/萬件.
萬元/萬件.
(1)將該產品的利潤![]() 萬元表示為促銷費用
萬元表示為促銷費用![]() 萬元的函數(shù);
萬元的函數(shù);
(2)促銷費用投入多少萬元時,廠家的利潤最大.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() 與
與![]() .
.
(1)若曲線![]() 與曲線
與曲線![]() 恰好相切于點
恰好相切于點![]() ,求實數(shù)
,求實數(shù)![]() 的值;
的值;
(2)當![]() 時,
時,![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍;
的取值范圍;
(3)求證:![]() .
. ![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】近年來,我國許多省市霧霾天氣頻發(fā),為增強市民的環(huán)境保護意識,某市面向全市征召![]() 名義務宣傳志愿者,成立環(huán)境保護宣傳組織,現(xiàn)把該組織的成員按年齡分成
名義務宣傳志愿者,成立環(huán)境保護宣傳組織,現(xiàn)把該組織的成員按年齡分成![]() 組第
組第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,得到的頻率分布直方圖如圖所示,已知第
,得到的頻率分布直方圖如圖所示,已知第![]() 組有
組有![]() 人.
人.

(1)求該組織的人數(shù);
(2)若在第![]() 組中用分層抽樣的方法抽取
組中用分層抽樣的方法抽取![]() 名志愿者參加某社區(qū)的宣傳活動,應從第
名志愿者參加某社區(qū)的宣傳活動,應從第![]() 組各抽取多少名志愿者?
組各抽取多少名志愿者?
(3)在(2)的條件下,該組織決定在這![]() 名志愿者中隨機抽取
名志愿者中隨機抽取![]() 名志愿者介紹宣傳經驗,求第
名志愿者介紹宣傳經驗,求第![]() 組至少有
組至少有![]() 名志愿者被抽中的概率.
名志愿者被抽中的概率.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com