【題目】某種產品的廣告費支出x與銷售額y(單位：百萬元)之間有如下的對應數據：
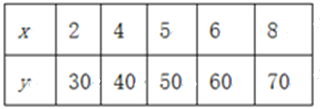
（1）請畫出上表數據的散點圖；
（2）請根據上表提供的數據，用最小二乘法求出y關于x的線性回歸方程
=
x+
；
（參考公式：用最小二乘法求線性回歸方程系數公式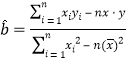 
，
．）
【答案】（1）見解析;（2）
【解析】試題分析：（1）根據表中所給的五組數據，得到五個點的坐標，在平面直角坐標系中畫出散點圖.(2 )先求出橫標和縱標的平均數，得到這組數據的樣本中心點，利用最小二乘法求出線性回歸方程的系數，代入樣本中心點求出
的值，寫出線性回歸方程.
試題解析：（1）散點圖如下圖所示：
（2）
，
，
，
，
，
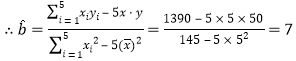所求回歸直線方程為
【方法點晴】本題主要考查散點圖的畫法和線性回歸方程，屬于難題.求回歸直線方程的步驟：①依據樣本數據畫出散點圖，確定兩個變量具有線性相關關系；②計算
的值；③計算回歸系數
；④寫出回歸直線方程為
；(2) 回歸直線過樣本點中心
是一條重要性質，利用線性回歸方程可以估計總體，幫助我們分析兩個變量的變化趨勢.
一線名師提優試卷系列答案科目：高中數學 來源： 題型：
【題目】已知函數f(x)= 
；
(1)若f(x)的定義域為 (－∞,+∞)， 求實數a的范圍；
(2)若f(x)的值域為 [0, +∞), 求實數a的范圍
查看答案和解析>>
科目：高中數學 來源： 題型：
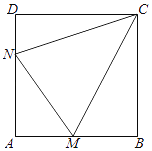
【題目】如圖所示，某村積極開展“美麗鄉村生態家園”建設，現擬在邊長為1千米的正方形地塊ABCD上劃出一片三角形地塊CMN建設美麗鄉村生態公園，給村民休閑健身提供去處．點M，N分別在邊AB，AD上． （Ⅰ）當點M，N分別是邊AB，AD的中點時，求∠MCN的余弦值；
（Ⅱ）由于村建規劃及保護生態環境的需要，要求△AMN的周長為2千米，請探究∠MCN是否為定值，若是，求出此定值，若不是，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某電視臺舉行電視奧運知識大獎賽，比賽分初賽和決賽兩部分．為了增加節目的趣味性，
初賽采用選手選一題答一題的方式進行，每位選手最多有
次選題答題的機會，選手累計答對
題或答錯題即終止其初賽的比賽，答對題者直接進入決賽，答錯題者則被淘汰．已知選手甲答題的正確率為
．
(1) 求選手甲可進入決賽的概率；
(2) 設選手甲在初賽中答題的個數為
，試寫出的分布列，并求的數學期望．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓
，圓
，動圓
與圓
外切并與圓
內切，圓心
的軌跡為曲線
.
（1）求
的方程；
（2）
是與圓
，圓
都相切的一條直線，
與曲線
交于
兩點，當圓
的半徑最長時，求
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
（a＞0，a≠1，m≠﹣1），是定義在（﹣1，1）上的奇函數．
（I）求f（0）的值和實數m的值；
（II）當m=1時，判斷函數f（x）在（﹣1，1）上的單調性，并給出證明；
（III）若
且f（b﹣2）+f（2b﹣2）＞0，求實數b的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知奇函數
在區間
上是增函數，且最大值為10，最小值為4，則在區間
上
的最大值、最小值分別是( )
A. -4,-10 B. 4,-10
C. 10,4 D. 不確定
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
