已知向量
=(
,1),
=(0,-1),
=(t,
),若
-2
與
共線,則t=
.
考點:平面向量共線(平行)的坐標(biāo)表示
專題:平面向量及應(yīng)用
分析:由向量減法的坐標(biāo)運算及數(shù)乘運算求得若
-2
的坐標(biāo),再由向量共線的坐標(biāo)表示列式求得t的值.
解答:
解:∵
=(
,1),
=(0,-1),
∴
-2
=
(,1)-2(0,-1)=(,3),
又
=(t,
),且
-2
與
共線,
則
×-3t=0,解得:t=1.
故答案為:1.
點評:平行問題是一個重要的知識點,在高考題中常常出現(xiàn),常與向量的模、向量的坐標(biāo)表示等聯(lián)系在一起,要特別注意垂直與平行的區(qū)別.若
=(a
1,a
2),
=(b
1,b
2),則
⊥
?a
1a
2+b
1b
2=0,
∥
?a
1b
2-a
2b
1=0,是基礎(chǔ)題.
練習(xí)冊系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來源:
題型:
已知函數(shù)若x,y滿足約束條件
,目標(biāo)函數(shù)z=ax+2y僅在點(1,0)處取得最小值,則實數(shù)a的取值范圍是( )
| A、(-4,2) |
| B、(-4,1) |
| C、(-∞,-4)∪(2,+∞) |
| D、(-∞,-4)∪(1,+∞) |
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:
題型:
設(shè)數(shù)列
,
,2
,
,…,則2
是這個數(shù)列的( )
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:
題型:
如圖是某樣本數(shù)據(jù)的莖葉圖,則該樣本數(shù)據(jù)的眾數(shù)為( )
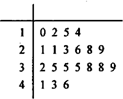
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:
題型:
經(jīng)過點(2,1),且傾斜角為135°的直線方程為( )
| A、x+y-3=0 |
| B、x-y-1=0 |
| C、2x-y-3=0 |
| D、x-2y=0 |
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:
題型:
已知圓C:x2-2x+y2=0.
(1)判斷直線l:x-y+1=0與圓C的位置關(guān)系;
(2)求過點(0,2)且與圓C相切的直線方程.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:
題型:
復(fù)數(shù)z=
,則z的共軛復(fù)數(shù)
在復(fù)平面內(nèi)對應(yīng)的點( )
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:
題型:
計算:
(1)(3+4i)+(-5-3i);
(2)(4-3i)(-5-4i);
(3)
;
(4)
-.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:
題型:
設(shè)函數(shù)f(x)=
logx,若數(shù)列:2,f(x
1),f(x
2),…,f(x
m),2m+4為等差數(shù)列,m∈N
*.
(Ⅰ)求數(shù)列{f(x
n)}(1≤n≤m,m、n∈N
*)的通項公式;
(Ⅱ求數(shù)列{x
n}(1≤n≤m,m、n∈N
*)的前n項和S
n.
查看答案和解析>>



 開心蛙狀元測試卷系列答案
開心蛙狀元測試卷系列答案