
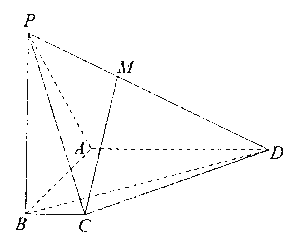
【題目】如圖,在三棱錐![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分別是
分別是![]() ,
,![]() 的中點,
的中點,![]() 在
在![]() 上且
上且![]() .
.
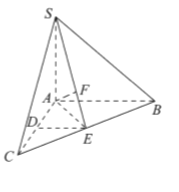
(I)求證:![]() ;
;
(II)求直線![]() 與平面
與平面![]() 所成角的正弦值;
所成角的正弦值;
(III)在線段![]() 上是否存在點
上是否存在點![]() ,使二面角
,使二面角![]() 的大小為
的大小為![]() ?若存在,求出
?若存在,求出![]() 的長;若不存在,請說明理由.
的長;若不存在,請說明理由.
【答案】I.見解析;Ⅱ.![]() ;Ⅲ.滿足條件的點G存在,且
;Ⅲ.滿足條件的點G存在,且![]()
【解析】
I:建立空間坐標系,求出相應(yīng)的直線的方向向量和平面的法向量,證明向量的平行即可;Ⅱ:求出平面SBD的法向量,直線SA的方向向量,由公式可得到線面角;Ⅲ.假設(shè)滿足條件的點G存在,并設(shè)DG=1.則G(1,t,0),求出平面AFG的法向量,和面AFE的法向量,由二面角的平面角的公式得到關(guān)于t的方程,進而求解.
I.以A為坐標原點,分別以AC,AB.AS為x,y,z軸建立空間直角坐標系C-xyz.則A(0,0,0),B(0,2,0),C(2,0,0),S(0,0,2),D(1,0,0),E(1,1,0)
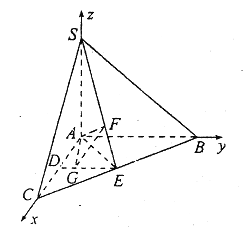
由SF=2FE得F(![]() ,
,![]() ,
,![]() )
)
![]()
![]() 平面
平面
![]()
![]()
![]() 平面SBC
平面SBC
Ⅱ.設(shè)![]() (x1,y1,z1)是平面SBD的一個法向量,
(x1,y1,z1)是平面SBD的一個法向量,
由于![]() ,則有
,則有

令![]() ,則
,則![]() ,即
,即![]() 。
。
設(shè)直線SA與平面SBD所成的角為![]() ,而
,而![]() ,
,
所以
Ⅲ.假設(shè)滿足條件的點G存在,并設(shè)DG=![]() .則G(1,t,0).
.則G(1,t,0).
所以![]()
設(shè)平面AFG的法向量為![]() ,
,
則
取![]() ,得
,得![]()
即![]() .
.
設(shè)平面AFE的法向量為![]()
則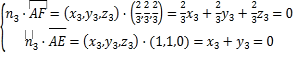
取![]() ,得
,得![]() ,即
,即![]()
由得二面角G-AF-E的大小為![]() 得
得
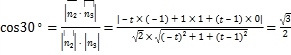 ,化簡得
,化簡得![]() ,
,
又![]() ,求得
,求得![]() ,于是滿足條件的點G存在,且
,于是滿足條件的點G存在,且![]()


科目:高中數(shù)學 來源: 題型:
【題目】如圖,在四棱錐![]() 中:
中:![]() 底面ABCD,底面ABCD為梯形,
底面ABCD,底面ABCD為梯形,![]() ,
,![]() ,且
,且![]() ,BC=1,M為棱PD上的點。
,BC=1,M為棱PD上的點。
(Ⅰ)若![]() ,求證:CM∥平面PAB;
,求證:CM∥平面PAB;
(Ⅱ)求證:平面![]() 平面PAB;
平面PAB;
(Ⅲ)求直線BD與平面PAD所成角的大小.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知8件不同的產(chǎn)品中有3件次品,現(xiàn)對它們一一進行測試,直至找到所有次品.
(1)若恰在第2次測試時,找到第一件次品,第6次測試時,才找到最后一件次品,則共有多少種不同的測試方法?
(2)若至多測試5次就能找到所有次品,則共有多少種不同的測試方法?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() 的左右頂點是雙曲線
的左右頂點是雙曲線![]() 的頂點,且橢圓
的頂點,且橢圓![]() 的上頂點到雙曲線
的上頂點到雙曲線![]() 的漸近線的距離為
的漸近線的距離為![]() 。
。
(1)求橢圓![]() 的方程;
的方程;
(2)若直線![]() 與
與![]() 相交于
相交于![]() 兩點,與
兩點,與![]() 相交于
相交于![]() 兩點,且
兩點,且![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ,(
,(![]() 為常數(shù))
為常數(shù))
(1)若![]()
①求函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的最大值及最小值。
上的最大值及最小值。
②若過點![]() 可作函數(shù)
可作函數(shù)![]() 的三條不同的切線,求實數(shù)
的三條不同的切線,求實數(shù)![]() 的取值范圍。
的取值范圍。
(2)當![]() 時,不等式
時,不等式![]() 恒成立,求
恒成立,求![]() 的取值范圍。
的取值范圍。
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,四棱錐P-ABCD中,側(cè)面PAD為等邊三角形且垂直于底面ABCD,![]() E是PD的中點.
E是PD的中點.
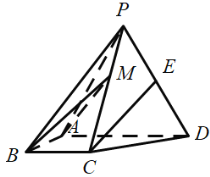
(1)證明:直線![]() 平面PAB;
平面PAB;
(2)點M在棱PC 上,且直線BM與底面ABCD所成角為![]() ,求二面角M-AB-D的余弦值.
,求二面角M-AB-D的余弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知二次函數(shù)f(x)的最小值為﹣4,且關(guān)于x的不等式f(x)≤0的解集為{x|﹣1≤x≤3,x∈R}.
(1)求函數(shù)f(x)的解析式;
(2)求函數(shù)g(x)![]() 的零點個數(shù).
的零點個數(shù).
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() .
.
(Ⅰ)若曲線![]() 在點
在點![]() 處的切線經(jīng)過點(0,1),求實數(shù)
處的切線經(jīng)過點(0,1),求實數(shù)![]() 的值;
的值;
(Ⅱ)求證:當![]() 時,函數(shù)
時,函數(shù)![]() 至多有一個極值點;
至多有一個極值點;
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】隨著智能手機的普及,使用手機上網(wǎng)成為了人們?nèi)粘I畹囊徊糠郑芏嘞M者對手機流量的需求越來越大.長沙某通信公司為了更好地滿足消費者對流量的需求,準備推出一款流量包.該通信公司選了5個城市(總?cè)藬?shù)、經(jīng)濟發(fā)展情況、消費能力等方面比較接近)采用不同的定價方案作為試點,經(jīng)過一個月的統(tǒng)計,發(fā)現(xiàn)該流量包的定價![]() :(單位:元/月)和購買人數(shù)
:(單位:元/月)和購買人數(shù)![]() (單位:萬人)的關(guān)系如表:
(單位:萬人)的關(guān)系如表:
![]()
(1)根據(jù)表中的數(shù)據(jù),運用相關(guān)系數(shù)進行分析說明,是否可以用線性回歸模型擬合![]() 與
與![]() 的關(guān)系?并指出是正相關(guān)還是負相關(guān);
的關(guān)系?并指出是正相關(guān)還是負相關(guān);
(2)①求出![]() 關(guān)于
關(guān)于![]() 的回歸方程;
的回歸方程;
②若該通信公司在一個類似于試點的城市中將這款流量包的價格定位25元/ 月,請用所求回歸方程預(yù)測長沙市一個月內(nèi)購買該流量包的人數(shù)能否超過20 萬人.
參考數(shù)據(jù):![]() ,
,![]() ,
,![]() .
.
參考公式:相關(guān)系數(shù)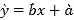 ,回歸直線方程
,回歸直線方程![]() ,
,
其中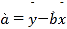 ,
,![]() .
.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com