
【題目】如圖,四邊形![]() 是邊長為2的菱形,且
是邊長為2的菱形,且![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 是線段
是線段![]() 上任意一點(diǎn).
上任意一點(diǎn).
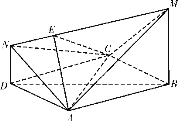
(1)證明:平面![]() 平面
平面![]() ;
;
(2)若![]() 的最大值是
的最大值是![]() ,求三棱錐
,求三棱錐![]() 的體積.
的體積.
【答案】(1)見證明;(2) ![]()
【解析】
(1)推導(dǎo)出AC⊥BM,AC⊥BD,得AC⊥平面BMND,從而可得到證明;(2)由AE=CE和余弦定理可知,當(dāng)AE最短即AE⊥MN,CE⊥MN時(shí)∠AEC最大,取MN中點(diǎn)H,連接H與AC、BD的交點(diǎn)O,知OH⊥平面ABCD,分別以直線![]() ,
,![]() ,
,![]() 為
為![]() 軸,
軸,![]() 軸,
軸,![]() 軸建立空間直角坐標(biāo)系,設(shè)
軸建立空間直角坐標(biāo)系,設(shè)![]() ,利用二面角
,利用二面角![]() 的平面角為
的平面角為![]() ,可求出a,然后利用VM﹣NAC=VM﹣EAC+VN﹣EAC可得結(jié)果.
,可求出a,然后利用VM﹣NAC=VM﹣EAC+VN﹣EAC可得結(jié)果.
(1)因?yàn)?/span>![]() 平面
平面![]() ,則
,則![]() .
.
又四邊形![]() 是菱形,則
是菱形,則![]() ,又
,又![]() ,
,
所以![]() 平面
平面![]() ,因?yàn)锳C在平面
,因?yàn)锳C在平面![]() 內(nèi),
內(nèi),
所以平面![]() 平面
平面![]() .
.
(2)設(shè)![]() 與
與![]() 的交點(diǎn)為
的交點(diǎn)為![]() ,連結(jié)
,連結(jié)![]() . 因?yàn)?/span>
. 因?yàn)?/span>![]() 平面
平面![]() ,則
,則![]() ,又
,又![]() 為
為![]() 的中點(diǎn),則
的中點(diǎn),則![]() ,由余弦定理得
,由余弦定理得![]() ,
,![]() .當(dāng)AE最短時(shí)∠AEC最大,此時(shí)
.當(dāng)AE最短時(shí)∠AEC最大,此時(shí)![]() ,
,![]() ,
,![]() ,因?yàn)锳C=2,
,因?yàn)锳C=2,![]() ,OE=
,OE=![]() . 取MN的中點(diǎn)H,分別以直線
. 取MN的中點(diǎn)H,分別以直線![]() ,
,![]() ,
,![]() 為
為![]() 軸,
軸,![]() 軸,
軸,![]() 軸建立空間直角坐標(biāo)系,
軸建立空間直角坐標(biāo)系,
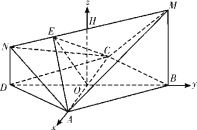
設(shè)![]() ,則點(diǎn)
,則點(diǎn)![]() ,
,![]()
![]() ,
,![]() ,
,![]() .設(shè)平面
.設(shè)平面![]() 的法向量
的法向量![]() ,
,
則 ,即
,即![]() ,取
,取![]() ,則
,則![]() ,
,
同理求得平面![]() 的法向量
的法向量![]() .
.
因?yàn)?/span>![]() 是二面角
是二面角 ![]() 的平面角,則
的平面角,則
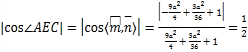 ,解得
,解得![]() 或
或![]() .
.
由圖可知a<OE=![]() ,故
,故![]() (舍去),
(舍去),![]() ,
,
因?yàn)?/span>![]() ,
,![]() ,
,![]() ,
,
則![]() .
.


 心算口算巧算一課一練系列答案
心算口算巧算一課一練系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)y=f(x)和y=g(x)在[-2,2]的圖像如圖所示,給出下列四個(gè)命題:

①方程f[g(x)]=0有且僅有6個(gè)根
②方程g[f(x)]=0有且僅有3個(gè)根
③方程f[f(x)]=0有且僅有5個(gè)根
④方程g[g(x)]=0有且僅有4個(gè)根
其中正確的命題是___
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)求曲線![]() 在點(diǎn)
在點(diǎn)![]() 處的切線方程;
處的切線方程;
(2)求![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(3)若對于任意![]() ,都有
,都有![]() ,求實(shí)數(shù)
,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() ,給定
,給定![]() 個(gè)整點(diǎn)
個(gè)整點(diǎn)![]() ,其中
,其中![]() .
.
(Ⅰ)當(dāng)![]() 時(shí),從上面的
時(shí),從上面的![]() 個(gè)整點(diǎn)中任取兩個(gè)不同的整點(diǎn)
個(gè)整點(diǎn)中任取兩個(gè)不同的整點(diǎn)![]() ,求
,求![]() 的所有可能值;
的所有可能值;
(Ⅱ)從上面![]() 個(gè)整點(diǎn)中任取
個(gè)整點(diǎn)中任取![]() 個(gè)不同的整點(diǎn),
個(gè)不同的整點(diǎn),![]() .
.
(i)證明:存在互不相同的四個(gè)整點(diǎn)![]() ,滿足
,滿足![]() ,
,![]() ;
;
(ii)證明:存在互不相同的四個(gè)整點(diǎn)![]() ,滿足
,滿足![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某種“籠具”由內(nèi),外兩層組成,無下底面,內(nèi)層和外層分別是一個(gè)圓錐和圓柱,其中圓柱與圓錐的底面周長相等,圓柱有上底面,制作時(shí)需要將圓錐的頂端剪去,剪去部分和接頭忽略不計(jì),已知圓柱的底面周長為![]() ,高為
,高為![]() ,圓錐的母線長為
,圓錐的母線長為![]() .
.
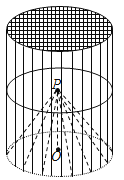
(1)求這種“籠具”的體積(結(jié)果精確到0.1![]() );
);
(2)現(xiàn)要使用一種紗網(wǎng)材料制作50個(gè)“籠具”,該材料的造價(jià)為每平方米8元,共需多少元?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
![]() Ⅰ
Ⅰ![]() 若函數(shù)
若函數(shù)![]() 的最大值為3,求實(shí)數(shù)
的最大值為3,求實(shí)數(shù)![]() 的值;
的值;
![]() Ⅱ
Ⅱ![]() 若當(dāng)
若當(dāng)![]() 時(shí),
時(shí),![]() 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
![]() Ⅲ
Ⅲ![]() 若
若![]() ,
,![]() 是函數(shù)
是函數(shù)![]() 的兩個(gè)零點(diǎn),且
的兩個(gè)零點(diǎn),且![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為了研究國民收入在國民之間的分配,避免貧富過分懸殊,美國統(tǒng)計(jì)學(xué)家勞倫茨提出了著名的勞倫茨曲線,如圖所示.勞倫茨曲線為直線![]() 時(shí),表示收入完全平等,勞倫茨曲線為折線
時(shí),表示收入完全平等,勞倫茨曲線為折線![]() 時(shí),表示收入完全不平等.記區(qū)域
時(shí),表示收入完全不平等.記區(qū)域![]() 為不平等區(qū)域,
為不平等區(qū)域,![]() 表示其面積,
表示其面積,![]() 為
為![]() 的面積.將
的面積.將![]() ,稱為基尼系數(shù).對于下列說法:
,稱為基尼系數(shù).對于下列說法:
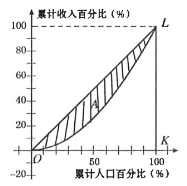
①![]() 越小,則國民分配越公平;
越小,則國民分配越公平;
②設(shè)勞倫茨曲線對應(yīng)的函數(shù)為![]() ,則對
,則對![]() ,均有
,均有![]() ;
;
③若某國家某年的勞倫茨曲線近似為![]() ,則
,則![]() ;
;
其中正確的是:( )
A.①②B.①③C.②③D.①②③
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在直三棱柱![]() 中,
中, ![]() 、
、![]() 分別為
分別為![]() 、
、![]() 的中點(diǎn),
的中點(diǎn), ![]() ,
, ![]() .
.
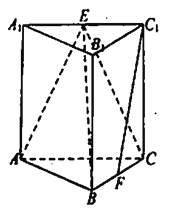
(1)求證:平面![]() 平面
平面![]() ;
;
(2)若直線![]() 和平面
和平面![]() 所成角的正弦值等于
所成角的正弦值等于![]() ,求二面角
,求二面角![]() 的平面角的正弦值.
的平面角的正弦值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com