
【題目】在直角坐標系![]() 中,曲線C的參數方程為
中,曲線C的參數方程為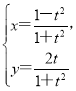 (t為參數),以坐標原點O為極點,x軸的正半軸為極軸建立極坐標系,直線
(t為參數),以坐標原點O為極點,x軸的正半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求C的普通方程和![]() 的直角坐標方程;
的直角坐標方程;
(2)求C上的點到![]() 距離的最大值.
距離的最大值.
【答案】(1)C的普通方程為![]() .
.![]() 的直角坐標方程為
的直角坐標方程為![]() (2)3
(2)3
【解析】
(1)把曲線C的參數方程平方相加可得普通方程,把x=ρcosθ,y=ρsinθ代入ρcosθ![]() ρsinθ+4=0,可得直線l的直角坐標方程;
ρsinθ+4=0,可得直線l的直角坐標方程;
(2)設出橢圓上動點的坐標(參數形式),再由點到直線的距離公式寫出距離,利用三角函數求最值.
(1)由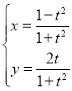 (t為參數),因為
(t為參數),因為![]() ,且
,且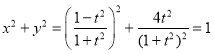 ,
,
所以C的普通方程為![]() .
.
由ρcosθ![]() ρsinθ+4=0,得x
ρsinθ+4=0,得x![]() y+4=0.
y+4=0.
即直線l的直角坐標方程為得x![]() y+4=0;
y+4=0;
(2)由(1)可設C的參數方程為![]() (
(![]() 為參數,
為參數,![]() ).
).
則P到直線得x![]() y+4=0的距離為:
y+4=0的距離為:
C上的點到![]() 的距離為
的距離為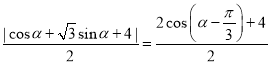 .
.
當![]() 時,
時,![]() 取得最大值6,故C上的點到
取得最大值6,故C上的點到![]() 距離的最大值為3.
距離的最大值為3.


科目:高中數學 來源: 題型:
【題目】某企業在“精準扶貧”行動中,決定幫助一貧困山區將水果運出銷售.現有8輛甲型車和4輛乙型車,甲型車每次最多能運6噸且每天能運4次,乙型車每次最多能運10噸且每天能運3次,甲型車每天費用320元,乙型車每天費用504元.若需要一天內把180噸水果運輸到火車站,則通過合理調配車輛,運送這批水果的費用最少為( )
A.2400元B.2560元C.2816元D.4576元
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】鳳鳴山中學的高中女生體重![]() (單位:kg)與身高
(單位:kg)與身高![]() (單位:cm)具有線性相關關系,根據一組樣本數據
(單位:cm)具有線性相關關系,根據一組樣本數據![]() (
(![]() ),用最小二乘法近似得到回歸直線方程為
),用最小二乘法近似得到回歸直線方程為![]() ,則下列結論中不正確的是( )
,則下列結論中不正確的是( )
A.![]() 與
與![]() 具有正線性相關關系
具有正線性相關關系
B.回歸直線過樣本的中心點![]()
C.若該中學某高中女生身高增加1cm,則其體重約增加0.85kg
D.若該中學某高中女生身高為160cm,則可斷定其體重必為50.29kg.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將數列![]() 的前
的前![]() 項分成兩部分,且兩部分的項數分別是
項分成兩部分,且兩部分的項數分別是![]() ,若兩部分和相等,則稱數列
,若兩部分和相等,則稱數列![]() 的前
的前![]() 項的和能夠進行
項的和能夠進行![]() 等和分割.
等和分割.
(1)若![]() ,試寫出數列
,試寫出數列![]() 的前
的前![]() 項和所有等和分割;
項和所有等和分割;
(2)求證:等差數列![]() 的前
的前![]() 項的和能夠進行
項的和能夠進行![]() 等和分割;
等和分割;
(3)若數列![]() 的通項公式為:
的通項公式為:![]() ,且數列
,且數列![]() 的前
的前![]() 項的和能夠進行等和分割,求所有滿足條件的
項的和能夠進行等和分割,求所有滿足條件的![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() ,函數
,函數![]()
(1)若![]() ,求出函數
,求出函數![]() 在區間上
在區間上![]() 的最大值.
的最大值.
(2)若![]() ,求出函數
,求出函數![]() 的單調區間(不必證明)
的單調區間(不必證明)
(3)若存在![]() ,使得關于
,使得關于![]() 方程
方程![]() 有三個不相等的實數根,求出實數
有三個不相等的實數根,求出實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線C的參數方程為
中,曲線C的參數方程為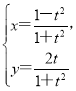 (t為參數),以坐標原點O為極點,x軸的正半軸為極軸建立極坐標系,直線
(t為參數),以坐標原點O為極點,x軸的正半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求C的普通方程和![]() 的直角坐標方程;
的直角坐標方程;
(2)求C上的點到![]() 距離的最大值.
距離的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)若![]() ,
,![]() ,求
,求![]() 的值域;
的值域;
(2)當![]() 時,求
時,求![]() 的最小值
的最小值![]() ;
;
(3)是否存在實數![]() 、
、![]() ,同時滿足下列條件:①
,同時滿足下列條件:① ![]() ;② 當
;② 當![]() 的定義域為
的定義域為![]() 時,其值域為
時,其值域為![]() .若存在,求出
.若存在,求出![]() 、
、![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列六個命題:
(1)若![]() ,則函數
,則函數![]() 的圖像關于直線
的圖像關于直線![]() 對稱.
對稱.
(2)![]() 與
與![]() 的圖像關于直線
的圖像關于直線![]() 對稱.
對稱.
(3)![]() 的反函數與
的反函數與![]() 是相同的函數.
是相同的函數.
(4)![]() 無最大值也無最小值.
無最大值也無最小值.
(5)![]() 的最小正周期為
的最小正周期為![]() .
.
(6)![]() 有對稱軸兩條,對稱中心有三個.
有對稱軸兩條,對稱中心有三個.
則正確命題的個數是( )
A.1個B.2個C.3個D.4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com