
【題目】已知F1 , F2是橢圓 ![]() (a>b>0)的兩個焦點,O為坐標原點,點P(﹣1,
(a>b>0)的兩個焦點,O為坐標原點,點P(﹣1, ![]() )在橢圓上,且
)在橢圓上,且 ![]()
![]() =0,⊙O是以F1F2為直徑的圓,直線l:y=kx+m與⊙O相切,并且與橢圓交于不同的兩點A,B
=0,⊙O是以F1F2為直徑的圓,直線l:y=kx+m與⊙O相切,并且與橢圓交于不同的兩點A,B
(1)求橢圓的標準方程;
(2)當 ![]()
![]() =λ,且滿足
=λ,且滿足 ![]() ≤λ≤
≤λ≤ ![]() 時,求弦長|AB|的取值范圍.
時,求弦長|AB|的取值范圍.
【答案】
(1)解:依題意,由 ![]()
![]() =0,可得PF1⊥F1F2,
=0,可得PF1⊥F1F2,
∴c=1,
將點p坐標代入橢圓方程可得 ![]() +
+ ![]() =1,又由a2=b2+c2,
=1,又由a2=b2+c2,
解得a2=2,b2=1,c2=1,
∴橢圓的方程為 ![]() +y2=1.
+y2=1.
(2)解:直線l:y=kx+m與⊙x2+y2=1相切,則 ![]() =1,即m2=k2+1,
=1,即m2=k2+1,
由直線l與橢圓交于不同的兩點A、B,設A(x1,y1),B(x2,y2),
由  ,得(1+2k2)x2+4kmx+2m2﹣2=0,
,得(1+2k2)x2+4kmx+2m2﹣2=0,
△=(4km)2﹣4×(1+2k2)(2m2﹣2)>0,化簡可得2k2>1+m2,
x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]() ,
,
y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2= ![]() =
= ![]() ,
,
![]() =x1x2+y1y2=
=x1x2+y1y2= ![]() =
= ![]() ,
,
![]() ≤
≤ ![]() ≤
≤ ![]() ,解可得
,解可得 ![]() ≤k2≤1,
≤k2≤1,
|AB|= ![]()
![]() =2
=2 ![]()
設u=k4+k2( ![]() ≤k2≤1),
≤k2≤1),
則 ![]() ≤u≤2,|AB|=2
≤u≤2,|AB|=2 ![]() =2
=2 ![]() ,u∈[
,u∈[ ![]() ,2]
,2]
分析易得, ![]() ≤|AB|≤
≤|AB|≤ ![]()
【解析】(1)依題意,易得PF1⊥F1F2 , 進而可得c=1,根據橢圓的方程與性質可得 ![]() +
+ ![]() =1,a2=b2+c2 , 聯立解可得a2、b2、c2的值,即可得答案;(2)根據題意,直線l與⊙x2+y2=1相切,則圓心到直線的距離等于圓的半徑1,即
=1,a2=b2+c2 , 聯立解可得a2、b2、c2的值,即可得答案;(2)根據題意,直線l與⊙x2+y2=1相切,則圓心到直線的距離等于圓的半徑1,即 ![]() =1,變形為m2=k2+1,聯立橢圓與直線的方程,即
=1,變形為m2=k2+1,聯立橢圓與直線的方程,即  ,得(1+2k2)x2+4kmx+2m2﹣2=0,設由直線l與橢圓交于不同的兩點A(x1 , y1),B(x2 , y2),則△>0,解可得k≠0,可得x1+x2=﹣
,得(1+2k2)x2+4kmx+2m2﹣2=0,設由直線l與橢圓交于不同的兩點A(x1 , y1),B(x2 , y2),則△>0,解可得k≠0,可得x1+x2=﹣ ![]() ,x1x2=﹣
,x1x2=﹣ ![]() ,進而將其代入y1y2=(kx1+m)(kx2+m)可得y1y2關于k的表達式,又由
,進而將其代入y1y2=(kx1+m)(kx2+m)可得y1y2關于k的表達式,又由 ![]() =x1x2+y1y2=
=x1x2+y1y2= ![]() =
= ![]() ,結合題意
,結合題意 ![]() ≤λ≤
≤λ≤ ![]() ,解可得
,解可得 ![]() ≤k2≤1,根據弦長公式可得|AB|=2
≤k2≤1,根據弦長公式可得|AB|=2 ![]() ,設u=k4+k2(
,設u=k4+k2( ![]() ≤k2≤1),則
≤k2≤1),則 ![]() ≤u≤2,將|AB|用u表示出來,由u
≤u≤2,將|AB|用u表示出來,由u ![]() [
[ ![]() ,2]分析易得答案.
,2]分析易得答案.


 開心快樂假期作業暑假作業西安出版社系列答案
開心快樂假期作業暑假作業西安出版社系列答案 名題訓練系列答案
名題訓練系列答案科目:高中數學 來源: 題型:
【題目】在等差數列{an}中,a1=2,a3+a5=16. (Ⅰ)求數列{an}的通項公式;
(Ⅱ)如果a2 , am , a2m成等比數列,求正整數m的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知一組數據的頻率分布直方圖如圖所示.求眾數、中位數、平均數( ) 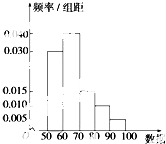
A.63、64、66
B.65、65、67
C.65、64、66
D.64、65、64
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列各組函數是同一函數的是( )
① ![]() 與
與 ![]() ;
;
②f(x)=x與 ![]() ;
;
③f(x)=x0與 ![]() ;
;
④f(x)=x2﹣2x﹣1與g(t)=t2﹣2t﹣1.
A.①②
B.①③
C.③④
D.①④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在正四棱錐S﹣ABCD中,O為頂點在底面內的投影,P為側棱SD的中點,且SO=OD,則直線BC與平面PAC的夾角是( )
A.30°
B.45°
C.60°
D.75°
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,拋物線關于x軸對稱,它的頂點在坐標原點,點P(1,2),A(x1 , y1),B(x2 , y2)均在拋物線上. 
(1)寫出該拋物線的方程及其準線方程;
(2)當PA與PB的斜率存在且傾斜角互補時,求y1+y2的值及直線AB的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2+2ax+2,x∈[﹣5,5].
(1)當a=﹣1時,求函數f(x)的最大值和最小值.
(2)函數y=f(x)在區間[﹣5,5]上是單調函數,求實數a的范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com